Dobrý den, potřeboval bych nastínit postup řešení následujícího příkladu. Nechci po Vás výpočet nebo tak, aby se neřeklo, že si sem píšu o řešení, ale jsem z toho bezradný a potřeboval bych nastínit, alespoň jak začít.
Zadání:
tg x = - 3/4
Děkuji za případné odpovědi a rady k mému problému
0x
Tak tady obecně vzato nezbývá než vzít kalkulačku nebo nahlédnout do tabulek. Anebo napsat řešení šalamounsky jako x = arctg–¾, (to je hlavní hodnota), nebo úplněji x = arctg–¾ + kπ. k cel= (případně v modifikaci: x = –arctg¾ + kπ.
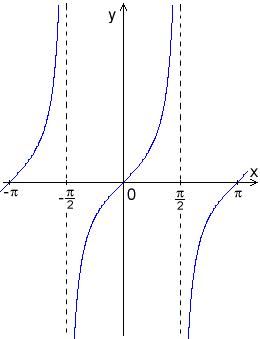
Funkce tangents je funkce periodická, jejíř graf (viz obrázek¨se opakuje, jako každá goniometrická funkce, s periodou 2π, a když se podíváte na obrázek, tak vidíte, že dokonce s periodou π, z obrázku je patrno, že akákoli přímka y = a (a reálné) protíná graf v pravě jednom bodě v pásu –π/2 < x < π/2, odpovídající x představuje hlavní řešení té rovnice a nazývá se arkustangents, a k tomu přistupují ta řešení posunutá o celé násobky pí. Ale nějaku "rozumnou" hodnotu má tangenta jen pro několik úhlů, třeba pro 45 stupňů je tangenta rovna 41, no a pro tyto pžípady pak můžete vaši rovnici vyřešit tak, jak si to asi představujete.
Obecně trochu záleží na tom, k jakému účelu chcete rovnici řešit. Pokud prostě je zadání "určete úhel alfa" a dopracujete se k jeho tangentě, můžete úlohu pokládat za vyřešenou či řešení "dokončit" pomocí kalkulačky. Pokud potřebujete s výsledkam dále pracovat, třeba potřebujete kosinus alfa, můžete případně použít vztahy mezi goniometrickými funkcemi, podle konkrétních požadavků.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.