Nejste přihlášen/a.
Dobrý den, mohli by jste mi poradit s tímto příkladem. Jsou to základy geniometrie.
Příklad se počítá na tag, tedy protilehlá ku přilehlé. Výsledek vyjde 42,9m Ten je správně!
Moje otázka: Dalo by se to počítat i přes cos tedy přilehlá ku přeponě. Tady výsledek vyjde 47,32, to je špatně.
Jak tedy přijdu na to, že se to má počítat přes tan a že con je špatně?
Děkuji
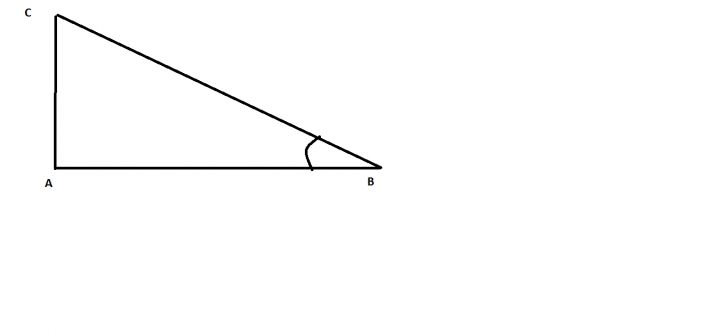
Na břehu řeky je zeměřena vzdálenost AB= 20m, kolmá na směr AC. . Z bodu B je vidět bod C na protějším břehu pod úhlem 650 . Jaká je vzdálenost bodů A, C?
2x
Počítá se to pomocí tangenty, protože je to přímočaré a evidentně nejjednodušší.Ale samozřejmě to lze počítat i pomocí cosinu a vyjde totéž,. i když postup bude samozřejmě složitější. (například budete muset spolupracovat s panem Pythagorem a řešit jednoduchou rovnici); přečtěte si, co vám k tomu píše Bruno. Pokud vám vyšlo něco jiného, není problém v ttom, jakou goniometrickou funkci používáte, ale jak ji používáte; mohl byste se nám svěřit, jak jste přišel na těch 47,2 m?
Ok děkuji.
přes cos jsem to počítal takto
cos650 = 20/x
cos650 *x = 20
x = 20/ cos650
x= 47,324
1x
Jak se to pozná? Musíš si uvědomit, které hodnoty znáš a kterou hodnotu chceš vypočítat. V zadaném příkladu máš pravoúhlý trojúhelník ABC, v něm je známá strana AB a úhel beta (sevřený stranami AB a BC). Máš vypočítat délku strany AC, tedy stranu, která je protilehlá úhlu beta. Pracuješ tedy s přilehlou stranou (20m) a neznámou protilehlou stranou. Nepracuješ s přeponou. Kosinus je poměr přilehlé strany k přeponě - jak bys mohla použít kosinus, když přeponu neznáš, ani je nechceš vypočítat? Už je to jasnější?
doplněno 21.03.15 22:12:Myslím, že tvůj problém spočívá v tom, že si neuvědomuješ, že tangens je poměr protihlehlé odvěsny k přilehlé odvěsně, kdežto kosinus je poměr protilehlé odvěsny k (přilehlé) přeponě. A ty přece hledáš délku protilehlé odvěsny a ne délku přepony.
doplněno 22.03.15 06:29:Pardon, chyba se vloudila: kosinus není poměr protilehlé odvěsny k (přilehlé) přeponě, nýbrž přilehlé odvěsny k přeponě. Tak ještě jednou: znáš úhel a k němu přilehlou odvěsnu a hledáš protilehlou odvěsnu. Takže nejjednodušší řešení (jak píše Kartaginec) spočívá v použití tangenty. Sinus a kosinus použiješ tehdy, když znáš nebo hledáš přeponu.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.