Zadání v obrázku...
moje úvaha... ![]()
možnost D by nejspíš platila
máme přímku, 2 body A,B , ... dáme 80 bodů kdekoliv na přímce kromě bodů AB a 10 bodů na jeden z těchto bodů
ale můžeme klidně dát 90 bodů na stejné místo jako bod A, a 80 bodů na stejné místo jako bod B :D to znamená, že by tam bylo 170 bodů :o takže nejde určit přesný počet... ale 90 by bylo pravdivé... :D tak nevím :/
3x
Autor příkladu asi nepočítal s tím, že vyznačíš třeba 5 bodů na to samé místo, ale že každý bod bude jinde.
Řešení je 22 bodů, pokud si je označíš vzestupně jako A-V, tak ty dva vnitřní jsou bod F(vnitřní bod 80 úseček) a bod G(90) (zrcadlově druhá taková dvojice je i P(90) a Q(80)).
Já to "řešil" v excelu
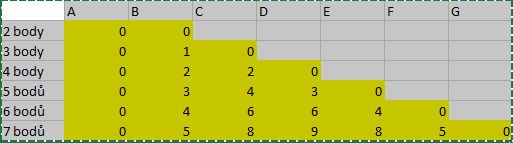
děkuji, už si to dokážu představit
takže teď záleží jen na tom, jestli autor vážně nepočítal s více body na jednom místě :D Což asi nepočítal :D
Ale v zadání není nijak zakázáno dát 2 body na stejné místo :D
Hodně důležité je podle mně slovo "bylo" v poslední větě. Nemůžu určit jednu hodnotu, kolik bodů tam bylo. Pokud by "bylo" změnili na "mohlo být", tak je odpověď 22 :D
Já vycházel z toho, že když jsou body A a C na stejném místě, tak neexistuje přímka CY, které by byl bod A vnitřním bodem.
Jak říkám jinde, počet bodů je počet bodů, ať mají jakoukoli funkci. Jistě, autor by mohl napsat "bylo modře vyznačeno několik různých bodů" nebo něco v tom smyslu, tak chcete-li, představte si tam toto upřesnění. Jistě, někdy se říká třeba "zvolme dva různé body " ale na otázku "kolik bodů jsi zvolil" odpovím vždy skutečným počtem.
prosím povíš mi jak by to v tom případě vypadalo? ![]()
já našel jen s těmi 90ti - z možností
v mém případě
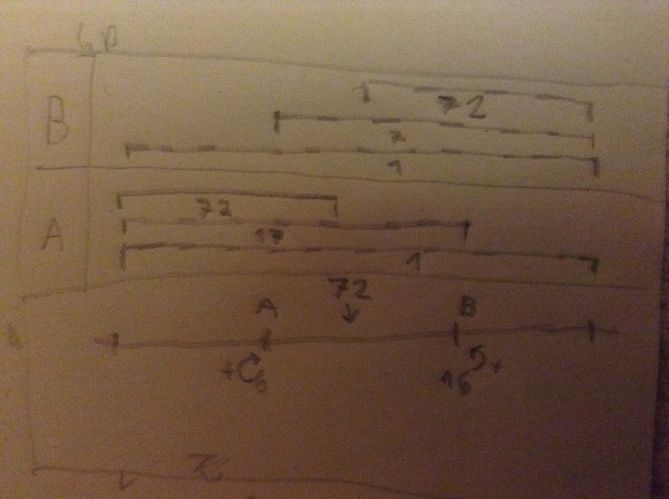
2 body na okraji, uvnitř body A, B -> 4 body
na stejném místě jako je bod A je dalších 6 bodů -> 7 bodů
na stejném místě jako bod B je dalších 16 bodů -> 17 bodů
mezi body A,B je 72 bodů
celkem 90 bodů
ve vrchní části označuji úsečky (jejich umístění), kterých je daný bod vnitřním bodem a jejich počet
pokud bude pravdivá moje i tvá varianta, znamená to, že by byla odpověď "nelze určit" ![]()
děkuji, palusus
doplněno 22.03.15 12:40:přepočítal jsem se, je tady 98 bodů... ani sčítání do 100 neumím :D
Varianrta 90 nemůže být pravdivá. Snedný rozbor, při němž počítám , že mám x bodů vlevo a y vpravo od toho kritického bodu, co leží uvnitř oasmdesáti pžímek, ře počet je x+y+1 a že xy = 80, a součet takových bodů nebude větší neřž pro x = 1 a y = 80, tedy cellkem 82.
Ostatně tato ůvaha by měla napomoci i k obecnému řešení, když ne jinak tak zkusmo.
doplněno 22.03.15 15:14:Klíčová je ovšem otázka, zda mohu měktyeré body počítat vícektrát. Co je to počet bodů? To je mohutnost , kardinální číslo, počet prvků množiny, tvořené těmito body, a každý bod té množiny je stále jeden prvek této množiny, ať ho počítáte, kolikrát chcete. Třeba obarvíte- li ze tří bodů dva na červeno a dva na modro, tak 2 + 2 = 4, ale ty body jsou stále jen tři, jen jeden znich bude dvoubarevný.
Vemte to třeba i takhle: připosťme na okamžik, že body A a B budeme počítat vícekrát. a podívejme se na vači konstrukci. budete-li k těm 72 vnitřním bodům přidávat či uvítrat nějaké body (což v jistém rozmezí mohu) a tuto zmašnu kompensovat odebráním či přidáním dvojnásobného počtu bodů, jednu sadu do body A a druhou do bodu B, nezmění se počet intervalů v kterých jsou body A a B uvnitř, ale celkový počet modrých bodů se bude měnit. Takhle by ta úloha byla dost nesmyslná, ne?
1x
Bod B leží na 90 úsečkách: (x+1+y)*z=90
Roznásobím a odečtu tyto 2 rovnice od sebe, dostanu:
(y+1)(z-x)=10
10=2*5 nebo 1*10
Takže y může být 1, 4, 0 nebo 9.
A tyto 4 varianty postupně vyzkouším a zjistím, že vyhovuje jen y=0.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.