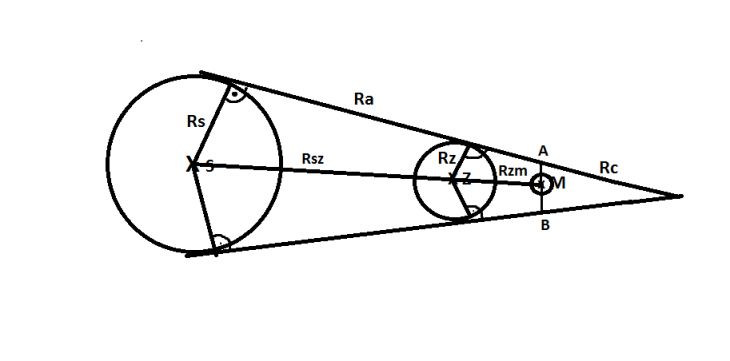
Potřebuji zjistit délku úsečky AB z náčrtku, znám hodnoty označené R.
0x
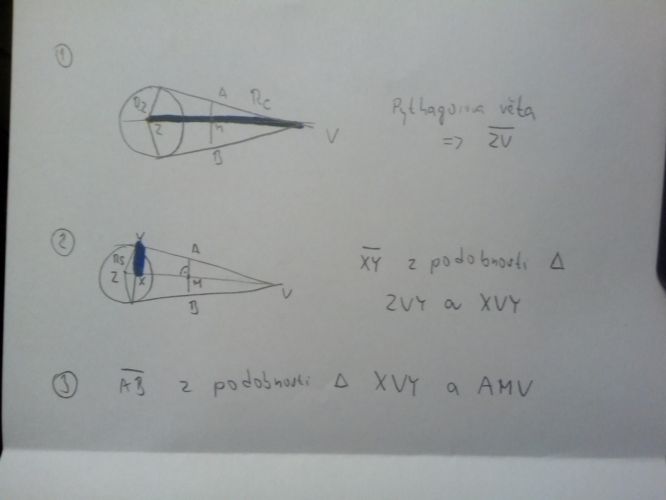
Rozdělím trojúhelník úplně vpravo (rovnoramenný trojúhelník, kdy ramnea jsou Rc a základna AB) na dva pravoúhlé trojúhelníky. Pomocí cosinu si vypočítám délku odvěsny, která je dělící čarou tohoto trojúhelníku. Úhel znám ten je 90°. No a potom pomocí c2=a2 b2 dopočítám půlku AB, vynásobím 2 a je to.
To tedy žasnu. Vždycky jsem myslel že v trojúhelníku je třeba znát tři údaje. A známe jenom pravý úhel a úsečku Rc
Přesněji "trojuhelnik" zná jenom pravý úhel a úsečku Rc. To by vskutku nestačilo, ale v obrázku toho je víc.
Takže asi takhle: Pro lepší domluvu bych ještě označil třeba V společný bod obou tečen a T bod dotyku té "horní" tečny /tedy krajní bod úsečky Ra).. Pak lze akceptovat trojuhelnikuv postup s tím, že ůhel. o který mu jde (a který se neobtěžoval spacifikovat) je ůhel SVT a jeho kosinus je roven Ra:|SV|. kde ůsečku |SV| explicitně neznám a musím ji počítat z Pythagorovy věty. Na druhou stranu bych do toho trigonometrii vůbec netahal. Je zřejmé, že trojůhelníky SVT a VAM se shodují ve dvou ůhlech a jsou tedy podobné, takže bych využil vztah |AM|:Rs = Rc: |SV|.
Jiná věc je, že v obrázku je zadáno mnohem více dat, než jsem využil, takže by se určitě daly najít i jině postupy.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.