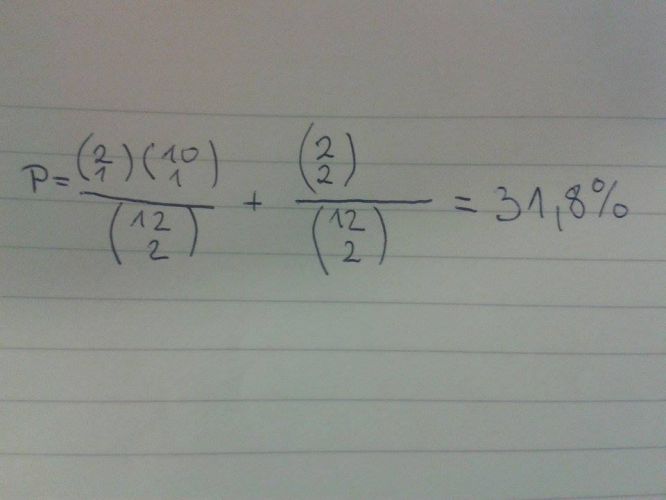Prosím poraďte, co dělám špatně.
Jaká je pravděpodobnost, že na dvou kostkách padne alespoň jedna šestka.
1x
Množina všech příznivých jevů je {[6, 1], [6, 2], [6, 3], [6, 4], [6, 5], [1, 6], [2, 6], [3, 6], [4, 6], [5, 6], [6, 6]}. Počet všech jevů je 6⋅6 = 36.
Pravděpodobnost bude 11/36 = 0,30555 ≐ 30,6 %
A proč by to tak mělo vyjít? můžete napsat, co jste si myslel, že počítáte, prostě nějaké zdůvodnění? Následně se podíváme, v čem je to zdůvodnění chybné-
Pravděpodobnost, že na první kostce padne 6 a na druhé ne, je 1/6*5/6 = 5/36.
Pravděpodobnost, že na první kostce nepadne 6 a na druhé ano, je 5/6*1/6 = 5/36.
Pravděpodobnost, že na obou kostkách padne 6, je 1/6*1/6 = 1/36.
Pravděpodobnost, že padne alespoň jedna šestka, je 5/36 + 5/36 + 1/36 = 11/36.
Ten váš postup by platil, kdybychom např. losovali z 12 karet, kde by 2 byly označeny 1, 2 označeny 2, 2 označeny 3, ... až 2 označeny 6. Zde jsou jednotlivé pokusy vzájemně závislé (výsledek v libovolném pokusu závisí na předcházejících pokusech) – P(A⋂B) ≠ P(A) ⋅ P(B).
Při hodu kostkami se jedná o nezávislé pokusy (pravděpodobnost výsledku na jedné kostce nezávisí na tom, co padlo na druhé kostce) – P(A⋂B) = P(A) ⋅ P(B).
0x
Omlouvám se, že do toho vstupuji, tyto matematické záležitosti mi nikdy moc nešly, ale mně to selským rozumem, bráno naprosto od boku, připadá takto: Pravděpodobnost, že na kostce padne šestka, je jedna ku šesti. Máme-li kostky dvě, je pravděpodobnost dvojnásobná, čili dvě ku šesti, neboli jedna ku třem, tudíž 33,333333...
Nebo uvažuji špatně?
No ale uvažte toto: podle stejné logiky by v případě, že máte šest sestek, byla pravděpodobnost šestkrát větší čili jistota, a to asi nebude pravda, ne?
Pravděpodobnost je prostě poměr , udávající , v kolika případech ze všech možných nastane ten, kerý je pro nás příznivý. Samozžřejmě když házím jednou kostkou, je pravděpodobnost 1/6, čili v průměru padne šestka v jedom případě ze šesti, ale to neznamené, že nemůže v dvaceti případech padnout něco jiného, ten poměr se realizuje až v dlouhé serii, podle zákona velkých čísel, ale to zde není až tak podstatné.
Jasně, jak už jsem řekl, tyhle výpočty vůbec neovládám, ze škol už jsem dávno pryč... Ten váš dodatek se šesti kostkami mě také hned napadl (mimochodem - jaká je tedy pravděpodobnost, že při hodu šesti kostkami padne alespoň jedna šestka?)
Je jasné, že při podobném uvažování by při hodu šedesáti kostkami byla pravděpodobnost 10:1, čili desetinásobná jistota, což je naprostá pitomost ![]() Proto mám v úctě všechny, kteří tento obor bravurně ovládají.
Proto mám v úctě všechny, kteří tento obor bravurně ovládají.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.