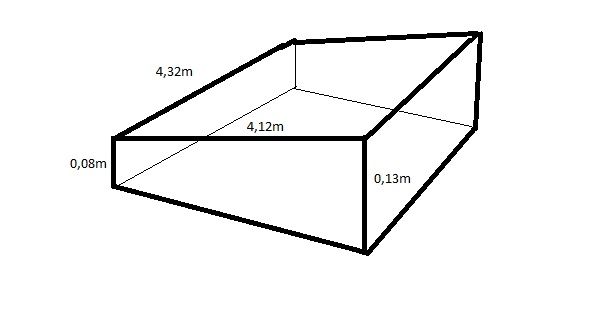
Zdravím lidi, potřebuju to sice pro stavebnictví, ale v podstatě je to geometrie. Prosím o vzorec, nebo výpočet obsahu a objemu obrazce na obrázku. Doufám, teda, že se dobře vyjadřuji potřebuju m3 a litry. Děkuju za každou radu. Na matematiku jsem strašně negramotný 
3x
No, jak nejjednodušeji? Udělejte z tohoto tvaru kvádr tak, že stejné těleso překlopíte na to Vaše. Jaký to bude mít tvar? (0,08 + 0,13) . 4,12 . 4,32 = 3,737664m³ a nyní to zpět vydělte dvěmi. A vyjde Vám 1,868832m³, což je 1868,832litrů... tak asi tak. 
Řekl bych, podle nákresu, že ta délka 4,12 m není tak úplně přesně délka jedné strany v tom myšleném kvádru (je to délka toho šikmého), ale o moc se lišit nebude, takže +/- bude i ten uvedený výsledek použitelný.
4,32 x 4,12 je ta vrchní strana, takže by to mělo být OK, bohužel materiál, který jsem měl v úmyslu na toto použít mi přijde v tomto množství docela "drahý" oproti jiné variantě.
Takže podlahu srovnám jinak na velikost 8cm, pak dám 4cm polystyrenu (cca 1.000,-Kč) a 4cm vaty (+/- 3.000,-Kč).
Původní varianta by byla liapor, který by vycházel 5.500,-Kč + k tomu geotextilie cca 22m2, která taky bude něco stát.
V obou variantách použiju ještě okrajové pásky.
Otázkou je, pokud výšku srovnám prkny tak na kolik mne vyjdou ty ... uvidíme..
Každopádně děkuju.
1x
Předpokládám, že pravé ůhly jsou u základny, tedy že jde o kolmý hranol, nahoře šikmo seříznutý. (A taky, že základna je obdélník, tedy pravoúhlý rovnoběžník.) Pak má nejspíč pravdu @hm, tedy že orientačně je Strejcův výpočet dostačující (jen bych nebazíroval na těch dvou desetinných místech. A navíc přesnější výpočet, zdá se, už není aktuální, ale kdyby byl, dala by se strana a toho základnového obdélníka, co není známa, vypočítat Pythagorem podle vzorce a2 = 4,122 = (0,13 – 0,05)2. Nicméně si neodpustím poznámku k jednotkám. V dotaze se ptáme na obsah a objem. Nuže, zatím jsme tu počítali objem, a to v kubících (tedy kmetrech na třetí; litr je kubický decimetr, tedy tisícina kubického metru. Obsah by se oak týkal pláště, případně povrchu, nevím, co konkrétně (a zda vůbec) tazatele zajímalo. Zdá se, že teď už nic, ale kdyby přece, bylo by třeba požadavek upřesnit.
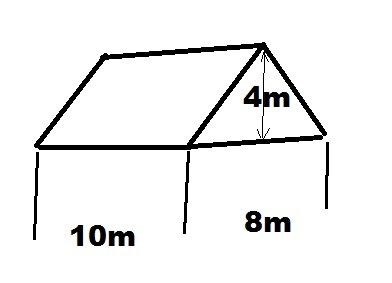
Ještě poprosím o rozlohu střechy, jsou to přibližné rozměry, ale +/- autobus by to mělo pro mé potřeby stačit, děkuju.
Primitivní pythagorova věta, ale bohužel jak jsem uvedl, jsem nějakou dobu ze školy a už i tam jsem to moc nedával. 
Vzoreček jsem nenašel abych si to zkusil 
podle vypocitejto.cz/...
když zadám a=4 b=4(m) tak = c=5,66
(10x5,66) x 2= 113,2m2 je to tak?
doplněno 11.03.15 12:49:c2=a2+b2
c2=42+42
c= odmocnica ze 32
c= zaokrouhleno 5,66m, takže by to mělo sedět
takže jen prosím o potvrzení, že je to OK?
Počítám-li obsah válce, tak při výšce 2m a průměru 0,05m to vychází podle vzorce
V=pí x průměr 2 x výška
V= 3,14 x 0,05(m) x 2(m)
V= 3,14 x 0,0025x2
V= 0,0157m3 tedy 15,7 litru
při výšce 2,5m to vychází na 19,6 litru říkám to dobře?
Ne.
1) Zřejmě se jedná o objem, ne o obsah (obsah je plocha, takže obsah bych chápal spíš jako velikost plechu pro vytvoření toho válce; u těles ale nepoužíváme "obsah", ale "povrch").
2) V = pí * poloměr2 * výška
poloměr = průměr / 2
takže: V = 3,14 * 0,0252 * 2 [m3] = 0,004 m3 = 4 litry
Při výšce 2,5 m by byl objem asi 5 litrů.
Jestli těch 5 cm je poloměr a ne průměr, tak to máš vypočítané správně, jen jsi se špatně vyjádřil.
Při vší úctě Váš výpočet se mi nezdá, průměr 10cm a výška 2,5m musí mít víc, jak 5 litrů, vždyť dvoulitrová lahev má na výšku cca +/- 30cm a průměr bude kolem těch +/- 10cm. Takže při 2,5 metrech to musí být mnohem víc než 5 litrů
doplněno 11.03.15 18:49:pletu poloměr s průměrem, samozřemě průměr 10cm, poloměr 5cm
doplněno 11.03.15 19:21:to jsem celej já, říkám sever, myslím jih hlavně, že se to vyjasnilo 
tak asi proto mi nikdy nešla matematika 
jsem holt línej přemejšlet 
Opět Vás zdravím, potřeboval bych opět pomoct
když
10 521 646 = 100%
kolik % je 454 618?
cca +/- 21%?
Pro rychlou orientaci: 20 procent je pětina, tedy zhruba 2100000, což neodpovídá ani numericky (tedy jsou to úplně jiné cifry), ale dokonce ani řádově.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.