Nejste přihlášen/a.
Prosím o radu s příklady pro pátou třidu matematické olympiády, lámeme si nad tím hlavu a nevíme si rady.
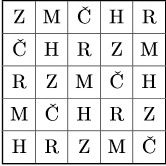
1 / Na obrázku je čtverec rozdělený na 25 čtverečků. Vybarvěte čtverečky pěti barvami tak, aby platilo: . každý čtvereček je vybarven jednou barvou, . v žádném řádku ani v žádném sloupci nejsou dva čtverečky stejné barvy, . na žádné z obou úhlopříček nejsou dva čtverečky stejné barvy, . žádné dva stejně barevné čtverečky se nedotýkají stranou ani vrcholem
2/ Na medaili, která má tvar kruhu o průměru 20 cm, je narýsován sněhulák tak, že jsou splněny následující požadavky: . sněhulák je složen ze tří kruhů jako na obrázku, . mezera nad sněhulákem je stejná jako pod ním, . průměry všech kruhů vyjádřené v cm jsou celočíselné, . průměr každého většího kruhu je o 2 cm větší než průměr kruhu předcházejícího. Určete výšku co největšího sněhuláka s uvedenými vlastnostmi.
obrázky jsou na této stránce: mo.webcentrum.muni.cz/...
jedná se o úlohy Z5 I-5 a Z5 I-6
Děkuji
3x
Nejmenší je horní kruh představující hlavu sněhuláka. Prostřední kruh je
o 2 cm větší než nejmenší kruh a spodní kruh je o 4 cm větší než nejmenší kruh. Celková
výška sněhuláka je tedy rovna třem průměrům nejmenšího kruhu a k tomu 6 cm.
Aby byla nad i pod sněhulákem ještě nějaká mezera, musí být výška sněhuláka menší
než 20 cm. To znamená, že tři průměry nejmenšího kruhu musí být menší než 14 cm, takže
průměr nejmenšího kruhu musí být menší nebo roven 4 cm (14 : 3 je 4, zbytek 2). Největší
sněhulák se všemi požadovanými vlastnostmi je tedy vysoký
3 . 4 + 6 = 18 (cm)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.