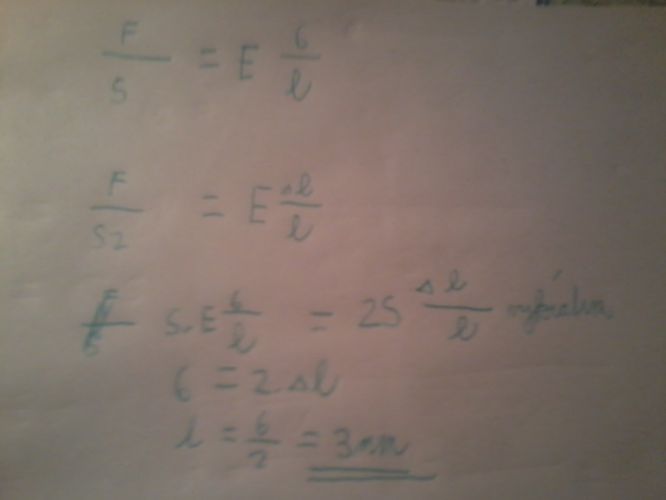Nejste přihlášen/a.
Dobrý den,, nebyl by někdo ochotnými poradit s těmito příklady? Vůbec si nevím rady.
Ten první příklad mám, ale ty další ne
Děkuji za pomoc.

2x
Prodloužení tyče pod mezí skluzu je dáno vzorcem x=F.l/S.E kde E=koeficient, vyjadřující pružnost materiálu v Pa. Podle tohoto vzorce prodloužení bude dvojnásobné oproti původním 6 mm, při dvojnásobné síle a délce, což jsou příklady 3 a 2. Naopak, bude poloviční při dvojnásobném průřezu, příklad 1.
Zamysli se nad tím a označ tedy správné řešení.
doplněno 01.02.15 19:46:Ano, dvojka je C. A trojka?
doplněno 01.02.15 21:49:3. příklad Síla F je ve vzorci v čitateli, proto je prodloužení přímo úměrné síle. 2x větší síla = 2x větší prodloužení. 2x6=12 mm
1. příklad vyjde opravdu 3 mm, protože síla je stejná.
----------------------------------------------------------------------------
Kartagiňanec> Napětí, které uvádíte, v zadání nikde nefiguruje. Napětí je podílem F/S, takže při dvojnásobném průřezu je poloviční a poloviční je pak i prodloužení.
doplněno 01.02.15 21:52:Výpočet na papíře máš dobře, ale nedá se to přečíst, tmavé, rozmazané, příště foť lepší, tohle je vražda to luštit. ![]()
Slovy: relativní prodloužení je úměrné napětí (koeficient E je Youngův modul pružnosti)
A možná bych upřesnil, že ta úměrnost platí pod mezí skluzu, ale pod mezí úměrnosti, která je obecně menší; ale to jsou terminologická upřesnění. Podstata výpočtu je vystižena přesně.
Proč myslíte, že A (3mm)? V tom vzorečku od dejavy je mezi prodloužením a silou přímá úměrnost, ne neúřímá.A v tom slovním popisu jsem psal o napětí, což je síla dělená průřezem a průřez je zde stejný v zadání a v trojce.
Add 2 a 3 asi nevyjde stejně( 12). Příde m divné mí 2x stejný výsledek.
0x
Ještě obecnou poznámku: všechny tyto příklady vycházejí z lineární teorie pryžnosti a předpokládají platnost Hookeova zákona, tedy z lineární závislosti mezi zatířením a prodloužením, respektive mezi napětím a relativním prodloužením. Vy jste patrně jinou teorii pružnosti ani nebrali a tuto linearitu předpokládáte a priori, ale když už tU padlo slovo "mez kluzu" (nikoli skluzu), tak k tomu něco řeknu.
Klasický Hookeův zákon vychází z pokusů. při nIchž zatěžujeme tyč z pružného materiálu, který se po "odtížení" vrací do původního stavu. Děláme-li tyto pokusy s materiály jako je ocel, guma a podobně, a "nepřeženeme-li" to, pokusy ukazují, že prodloužení (konkrétní zkoumané tyče) je lineárně úměrné zatížení (s konstantou úměrnosti, která závisí jednak na materiálu, jednak i na geometrii tyče. a takto vzniklá deformace není trvalá. Tohle neplatí například pro litinu, kde závislost není lineární (ale deformace nezůstává trvale), nebo plastické materiály (jako třeba plastická guma), kde tahem zdeformujeme materiál trvale; mezi tím jsou pružně-plastické materiály, u nichž jen část deformace (elastická deformace) zmizí a zůstane určitá trvalá, "plastická" zbytková deformace. (Takhle se chová i klasický pružný materiál, když ho zatížime příliš, překročíme "mez plasticity". Při odlehčení tyč zůstane delší, než byla původně, ovšem dojde obvykle ke zpevnění materiálu, při novém natahování se tyč zase bude chovat pružně, dokud nepřeročíma novou mez plasticity; ale to je jen takový hrubý nástin, teorie pružně-plastických deformací je poměrně dost komplikovaná.)
Takže vraťme se k tahové zkoušce dejme tomu ocelové homogenní tyče délky l, s plochou průřezu S, kterou budeme zatěžovat silou F. Je jasné, že žádná tyž není nezničitelná a tak pouhý "zdravý selský rozum" (jakkoli tuto frázi nemám příliš rád) naznačuje, že překročením jakéhosi kritického zatížení se tyč přetrhne a pokusům je konec. Tento fakt potvrzují i pokusy a vyplývá z nich existence kritické "mezi pevnosti", kterou je třeba u materiálů též experimentálně stanovit a počítat s ní při navrhování konstrukcí vzhledem k účelu a k předpokládanému (povolenému, maximálnímu) zatížení. Tahle mez ovšem není jednoznačně stanovitelná: není to tak, že až do dosažení této meze je konstrukce spolehlivá a při jejím překročení materiál okamžitě rupne. Musíme brát v úvahu "koeficient bezpečnosti", který je takový, že při dosažení mezní síly jemu odpovídající ještě materiál i dost dlouho vydrží (může být třeba i desetinásobný). Na to ale se teď vykašlu a budu myšlenkově popisovat chování tyče pod touto mezí; když říkám "myšlenkově", neznamená to, že si to chování vymýšlím, ale že pokus neprovádím fyzicky, leč popisuji to, co fyzicky prováděné pokusy ukázaly.
TEĎ JSEM TOHO ALE NAPLÁCAL DOST, TAKŽE TO ODEŠLU A POPIS POKUSU DODÁM V SAMOZTATNÉM POKRAČOVÁNÍ.
Jdeme na to. Budeme zkoumat homogenní ocelovou tyč délky l0, stálého průřezu S, zatíženou silou F. Zatížená tyč nechť má délku l, její (absolutní) prodloužení je tedy ∂l = (l –l0). (raději bych použil symbol Delteä l, ale pro velké Delta není v tabulce znaků poloha). Zajímá nás závislost síly F nea délce l, či ještě lépe na prodloužení ∂l.
Pokusy ukazují, že do určité velikosti zatěžující síly je závislost v tahovém diagramu lineární čili existuje konstanta K tak, že
F = K*∂l
Při stoupajícím zatížení závíslost přestává být lineární (mez úměrnosti), a v jistém okamžiku dojde dokonce k tomu, že materiál se prodlužuje, aniž by zatížení rostlo, nebo dokonce toto zatížení při zvětšujícím se prodloužení klesá (mez kluzu, též skluzu, dříve mez tečení – říkalo se, že při jejím překročení materiál teče). Tadu už jsme v mnohem složitější oblasti teorie a rozhodně se o ní nebudu bavit podrobněji. Ona už i ta lineární pružnost je vlastně dost složitá, uvědomme si například, že při protahování materiálu se zároveň zužuje průřez, což zanedbáváme.
Takže teď se vrátím k vztahu F = K*∂l . V tomto vztahu konstanta K závisí na materiálu, a tuto závislost musíme zjistit experimentálně. Kromě toho ale závisí i na geometrii tyče, tedy na l a na S, a tuto závislost nám pomůže dešifrovat následující úvaha:
Závislost na l. Představte si, že délku l zdvojnásobíme. Pak je situace stejná, jako když zavěsíme dvě tyče délku l za sebou, každá z nich je zatížena silou F a protáhne se tedy o ∂l a celkové protažení je dvojnásobné. To nás vede k závěru, že závislosti K na l se zbavíme, když nebudeme počítat absolutní prodloužení ∂l, ale relativní prodloužení (deformaci) ε = ∂l/l0. Takže přepíšeme-li vztak do podoby F = K1ε, nová konstanta úměrnosti už bude záviset na geometrii tyče jenprostřednictvím průřezu.
2. Takže co s průřezem? Jestliže ho zdvojnásobím, je to, jako bych vedle sebe položil dvě tyče stejné jako byly ty původní. Na rozdíl od zdvojnásobení délky ale teď musím tažnou sílu rozdělit, na každou půlku nové tyče bude působit jen její polovina . Takže místo sílý F je vhodné uvažovat napětí ρ= F/S (ono pro napětí se používá písmeno sigma, ale to nějak neumím, tak se omlouvám). A konečný tvar Hookeova zákona bude
ρ = E ε
kde nová konstanta E, nazývaná Youngův modul, už je opravdu jen a výhradné materiálová konstanta. Když do uvedeného vztahu dosadím ε = 1, což formálně znamená zdvojnásobení délky (proč formálně? protože se tím dostávám mimo pblast malých deformací, ve které jsme Hookeův zákon odvodili, a mezi námi, kterú materiál se dá nadáhnout dvojnásobně, aniž by rupnul? snad praková guma, ale rozhodně ne ocelová tyč), mohu říci, že jangův modul je napjetí, při kterém se délka tyče zdvojnásobí.
Ovšem, znovu zdůrazňuji, že jde o matematické zjednodušení, ale s tím vy jistě pracujete.
Děkuji moc, jste mi pomohl.
Ještě se zeptám na tuto úlohu.
Hliníková tyč má při teplotě 10 °C délku 2,0 m, objem 5,0.10-3m3 a hustotu 2 700 kg.m-3. Teplotní součinitel délkové roztažnosti hliníku je 24.10-6 K-1. Tyč zahřejeme na teplotu 60 °C.
Jakou hustotu má tyč při teplotě 60 °C?
Nevím, jak to spočítat. myslel, jsem, že to bude na vzorec V=V(1 + beta ( t-t)
Neporadil by jste mi vzoreček?
Děkuji
V zásadě je to tak, jen vám tam něco vypadlo (máte v závorce (t–t), což je nula), a taky by to chělo říci, co je to β. Takže ten vzoreček, který potřebujete, bude
V = V0(1+ β(t–t0))
kde V0 je objem telesa při teplotě t0, V je objem při teplotě t a β je koeficient objemové roztažnosti látky a je přibližně roven trojnásobku koeficientu délkové roztažnosti α, tedy
β≈3α.
Somozřejmě to platí v určitých mezích (minimálně t nemůže překročit bod tání), za předpokladu isotropie tělesa (má ve všech směrech stejné vlastnosti), a pochopitelně je to vše přibližné ("přesný" vzorec pro objemovou roztažnost, například, nebude bude lineární, ale kubický). Můžete se podívat i do Wikipedie, ovšem zrovna v tomhle článku to pověkud popletli, schválně, přijdete ne to, co tam mají špatně?
doplněno 04.02.15 14:47:To je tedy vzoreček objemové roztažnosti, "vzoreček" pro závislost hustoty na teplotě si musíte na jeho základě spočítat sám.
Především, F = M.G nic není, dokud nrřeknete, co je to F, co je to M a co je to ¨g; beztoho je to jen změť písmen. A co že to chcete vypočítat, Chcete vypočítat m? tím patrně máte na mysli hmotnost té tyče. Tu byste vypočítal z devinice hustoty podle vztahu m = V*ρ, kde ró je hustota, V je objem. To ale neptřebujete. Víte, že m je konstantní, tak tento vzorešek použijete pro teplotu 10 stupňů, kde znáte vše krom hmotnosti, pak pro teplotu 60 stupňů s použitím vzorce objemová roztažnosti a podělíte je, žímž se vám hmotnost vykrátí (a ještě něco se vykrátí).
Už to mám,
Teď snad poslední otázka.
U tyče z materiálu o modulu pružnosti E bylo při normálovém napětí σn zjištěno relativní prodloužení 0,2%.
1. Jaké je relativní prodloužení tyče při normálovém napětí 2σn?
a) 0,1 %
b) 0,2 %
c) 0,4 %
d) 0,8 %
2. Jaké je relativní prodloužení tyče z téhož materiálu při normálovém napětí σn, je-li délka tyče dvojnásobná?
a) 0,1 %
b) 0,2 %
c) 0,4 %
d) 0,8 %
3.Jaké je relativní prodloužení tyče při normálovém napětí σn, je-li tyč z materiálu o dvojnásobném modulu pružnosti v tahu tj. 2E?
a) 0,1 %
b) 0,2 %
c) 0,4 %
d) 0,8 %
1 příklad
Normálně bych to počítal podle Hookova zákona
normálové napětí = Eε
ε = 0,2%
normálové napětí = 2
proč mám zde vovu počítat ε, když ho již znám? Děkuji
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.