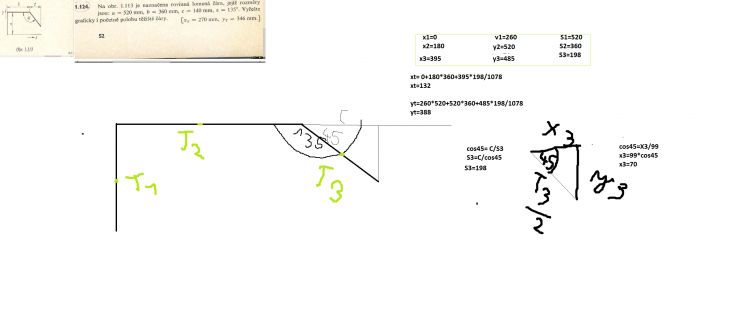
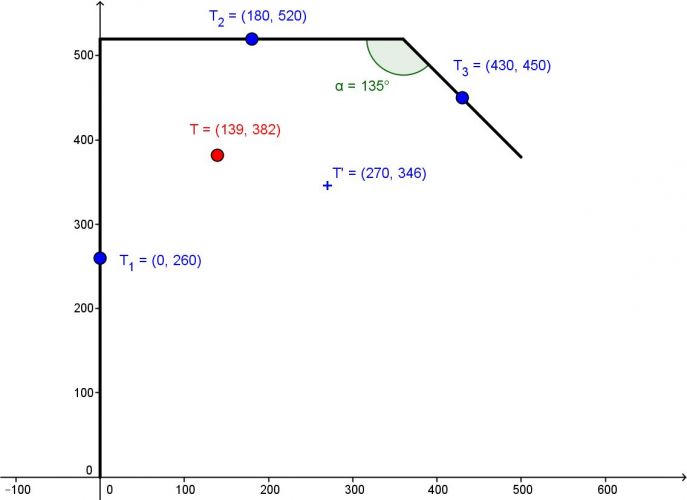
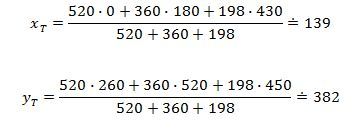Ahoj, potřeboval bych poradit s výpočtem těžiště čáry: v obrázku je zadání i to jak sem to počítal
Pokud by to někdo uměl počítat prosím napiště co sem tam udělal špatně, děkuji
3x
Blbě jsem četl obrázek (viz výše).
Ještě by to chtělo grafickou konstrukci, naznačil jsem postup v doplnění své odpovědi výše, snad dovede tazatel rozdělit úsečku graficky v poměru dvou daných úseček.
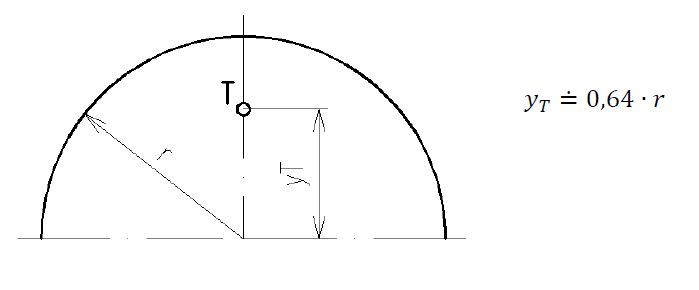
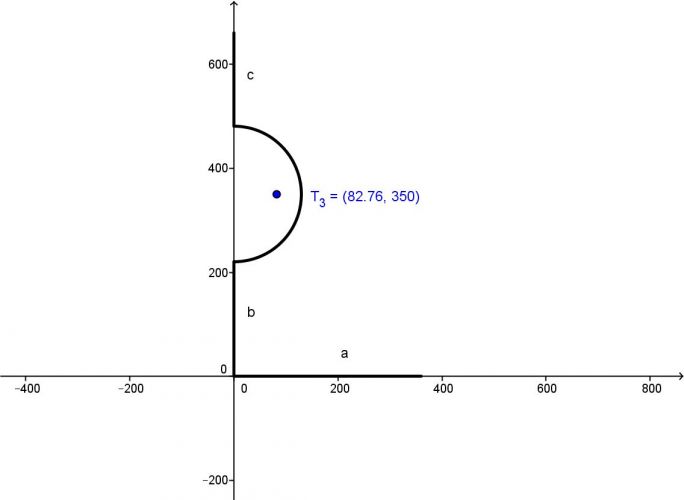
Dobrý den, děkuji za odpověď, a jestli máte čas mohl by ste mi ještě pomoc s jedným příkladem, nepotřebuji celý výpočet ,ale nevím co dělat s tou půlkružnicí jak vypočítat x3,y3 a l3 , zkoušel sem to tak že R je L3 , a x3 a y3 sem považoval za R/2 ,ale to nevycházelo, takže nevím co s tím dělat , učitel nám o tom nic neříkal :/
Když budete vědět tak prosím napište děkuji...
Zkuste se podívat sem.
doplněno 29.01.15 20:49:Ono obecně těžištč křivky je otázka integrálního počtu (křivkový integrál).
0x
Těžiště dvou čar leží na spojnici těžišť dvou čar. Spočteme polohu vektoru a následně spočteme těžiště výsledného vektoru s vektorem třetí čáry
Přiznám se, že pdle tohoto návodu bych to nedokázal;prostě se v tom neorientuji.
Ano, těžiště bude na spojnici obou těžišť, která musím brát tah, že jejich "váha" odpovídá délce příslušných úseček. To znamená, že těžiště T bude na spojnici T1 a T2 a bude úsečku T1T2 dělit v převráceném poměru k délkám u, v příslušných úseček"
|T1T| : |TT2| = v:u
z toho bych odvodil geometrickou konstrukci.
Početně bych postupoval tak, že nepříklad pro výpočet x-ové souřadnice bych souřednici T1,x násobil délkou u příslušné úsečky, k tomu bych připočetl T2,x násobeno délkou v té druhé úsečky a výsledek podělil součtem u + v.
Omlouvám se, že nerozeberu tazatelovo řešení, ono mi trochu dělá potíže, s mou kataraktou a makulární degenerací, ten obrázek rozšifrovat. Snad se toho ujme někdo jiný.
doplněno 29.01.15 19:01:Ty moje oči mají na svědomí chybu v mém postupu. Můj postup vucházel z předpokladu, že ta svislice není součástí lomené čáry (připadalo mi tenká) a údaj a jen určuje polohu, respektive je potřebný ka specifikaci ypsilovnvých souřednic. (I když váš obrázek byl jednoznařčný, ale já ho nebral do úvahy.) Takže postup, který jsem vám naznašik na výpočet, je dobře míněný, ale musí vzít v úvahu všechna tři těžiště, tak jak to napsal @x,
Grafický postup by byl nepatrně složitější, než jsem uváděl. Tedy, v podstatě stejný,,ale opakoval buch ho třikrát. respektivetělal bych těžiště trojúhelníka T1T2T3, v němž by ale vrcholy měly různou váhu, čili nespojoval bych vrchol se středem protilehlé strany, ale s jejím těžištěm (nalezeným ja popsáno výše).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.