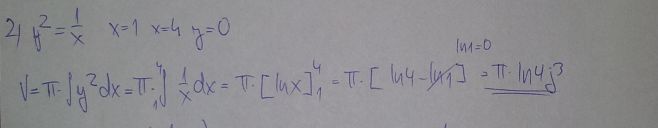Prosím může mi někdo zkotrolovat zda je ten příklad dobře? a pokud ano, proč se dosazují pokaždé jiné meze když v zadání je 0 a 4?
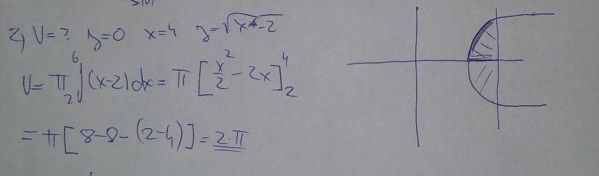
4x
Jak říká @x, v tom obrázku meze nejsou. Ten obrázek je spíše takový stenografický záznam, kterému rozumí jeho autor, pro nás je to tak trochu hádání z křišťálové koule. Nicméně se o to pokusím. Řekl bych (jak si myslí i @x), že máme počítat obsah vyšrafovaná části, a dovolím si popis doplnit podle svého odhadu: Spočtěte obsah obrazce, omezeného přímkami y = 0, x = 4 a horní větví paraboly y2 = x – 2. Pak je zřejmé to, co už napsal @x, že průsečík té paraboly s osou x (čili přímkou y = 0) je [2;0], obrazec leží tedy celý vpravo od tohoto bodu a z toho odvodíme dolní mez integrace x = 2. Jako omezení zprava bych bral tu přímku x = 4 a tedy integrační meze pro x jsou dolní mez 2, horní mez 4. Ta změna 4 → 6 je pak evidentně přepis.
Připojuji dva obrázky: jednak vyčištěný obrázek ze zadání, jednak jeho dopnění ve smyslu uvedeného popisu.
doplněno 18.01.15 18:46:A ještě poznámka: dle zadání máme počítat objem, tedy půjde ne o plošný obrazec, omezený tou parabolou, ale těleso, vzniklé rotací tohoto obrazce kolem osy y (další "těsnopis", který unikl mé křišřálové kouli). Proto to π před integrílem a proto integrujeme x–2 a ne odmocninu z tohoto výrazu.
doplněno 18.01.15 20:03:Pardon, samozřejmě kolem osy x.
doplněno 19.01.15 10:38:No a ještě samozřejmě ten pravý bod má být [4;0] a ne [2;4], moc se omlouvám.
moc děkuji za vysvětlení a mám tu ještě jeden stejný problém, opět nemám lepší zadání a nevím který výpočet je správně.
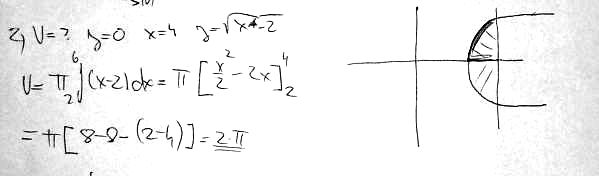
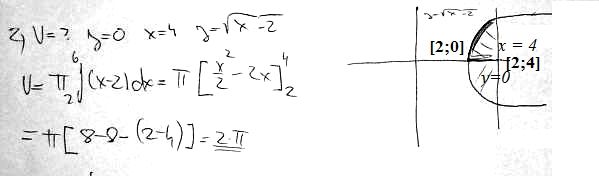
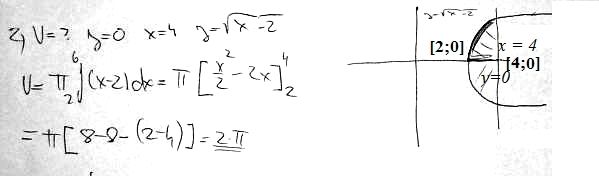
Zřejmě jde opět o objem rotačního tělesa, vzniklého rotací (kolem osy x) vyšrafovaného obrazce. omezeného přímkami x = 1, x = 4, y = 0 a křivkou y² = 1/x.
Obecně, objem rotačního tělesa vzniklého rotací obrazce omezeného křivkou y = f(x). osou x a přímkami x = a. x = b (a ≤b) je
V = πS f²(x)dx = πS y²dx
kde S jsem použil místo integřítka a beru ho v mezích od a do b. Při pohledu na obě zadání mi není jasné, co tam v tom druhém obrázku má znamenat to j³ (že by jednotky?), ale kduž ho vynechá, pak jsou správně oba výpočty (vždyť
ln 4 = ln 2² = 2*ln 2) a dokonce ten druhý mi přijde elegantnější (vynechal odmocnění a následné umocnění).
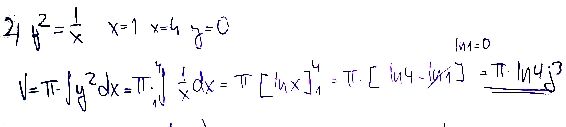
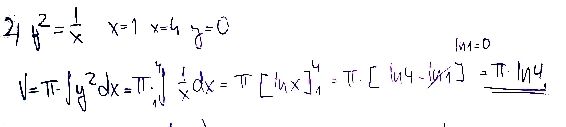
ten příklad jsem nepočítala já, proto se taky divim proč jsou vždy jiné meze. a zadaní mám jen to co je na tom obrázku.
Na náčrtku nejsou vyznačeny meze. Výsledek odpovídá integraci od 2 do 4. Ta 6 jako horní mez je zřejmě omyl.
Píšete: "zadaní mám jen to co je na tom obrázku". Na obrázku meze nevidím. Má-li se počítat objem vyšrafované části, tak je zřejmé, že graf začíná v bodě 2 (pro 2 je f(2) = 0), ale v kterém bodě vyšrafovaná část končí není určeno. Proč by mělo být zadání 0 až 4?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.