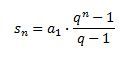Nejste přihlášen/a.
Pomůžete mi prosím někdo s tímto příkladem? Součet prvních jedenácti členů GP se rovná 683. Vypočítejte první a poslední člen, když q = -1/2. Předem děkuji.
2x
Jaké vzorce pro geomentrickou posloupnost známe? Označím-li a1 první člen, an je n-tý člen a q je kvocient, pak základní (vlastně definiční ) vzorec je
an+1 = q*an
(definice geometrické posloupnosti: podíl dvou sousedních členú nezávisí na n a nazývá se kvocient)
a připomenu další vzorce:
n-tý člen an = a1*qn–1
součet prvních n členů sn = a1 + ... + an = (1–qn+1)/(1–q)
( a případně součet nekonešné geometrické řady existuje pro |q| menší než jedna a je roven
s = a1 + a2 + ... = a1/(1–q) ; samozřejmě ta výsledná formulka má smisl i pro q větší než jedna, případně menší nebo rovno –1, ale pak to není součet geometrické řady.)
Požadované vypočteme, když do těchto vzorců dosadíme q = –½, s11 = 683.
(A jen na okraj: znak - není mínus. ale spojovník neboli divis. Jako mínus se používa pomlčka neboli n-dash – , což napíši jako pravý alt + 0150. On to skoro nikdo nebere na vědomí, ale typograficky je to zvrhlost.)
doplněno 18.01.15 12:57: Pardon, součet prvních n členů je sn = a1 + ... + an = (1–qn)/(1–q). To, co jsem napsal já, by byl součet prvních člené, kdybych začínal členem a0, tedy součet prvních n+1 členů:sn = a0 + ... + an = (1–qn+1)/(1–q).I tak to vypadá, že @x uvádí jiný vzores, ale to je totéž jen s přehozeným pořadím v čitateli i ve jmenovateli, což je lvastně dvakrát znásobeno mínus jednou.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.