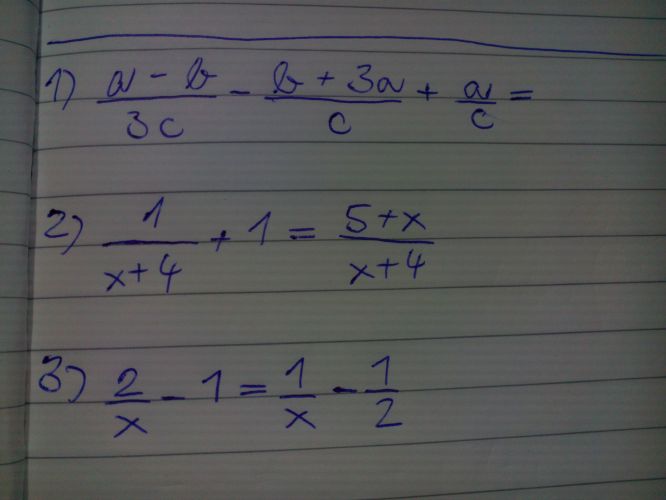Nejste přihlášen/a.
3x
Ahoj, musíš najít společné jmenovatele všech zlomků. Třeba u prvního to bude 3c. Tím pak vynásobíš celou rovnici, takže dostaneš a-b-3(b+3a)+3a. U druhého a třetího členu tam bude ta trojka, protože násobíš členy "3c", céčka se ti vyruší a na násobení tak zůstane jen ta trojka. Pak už jen sčítáš a odečítáš stejné se stejným. U ostatních je princip naprosto stejný. ![]()
Dokážeš sám určit ostatní společné jmenovatele? Jestli jo, tak máš vyhráno. ![]()
Tak jsem vyzkoušel vypočítat dle vaší rady a uspěšně, na společné taky vyšlo, Díky za vysvětlení Moc pomohlo ![]()
2x
To první vypadá jen jako výraz, ne rovnice. Tak to jen převeď na společného jmenovatele a uprav. Umíš to převést na společného jmenovatele?
Rovnice - tam vždycky vynásob obě strany (všechny členy) tím jmenovatelem, tím se ta proměnná dostane jen do "čitatelů" (resp. nebudou zlomky s proměnnou ve jmenovateli). A dál už upravíš normálně. Nezapomeň, že z přítomnosti proměnné ve jmenovateli pro ni vyplývají určité podmínky (aby tam nebyla 0).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.