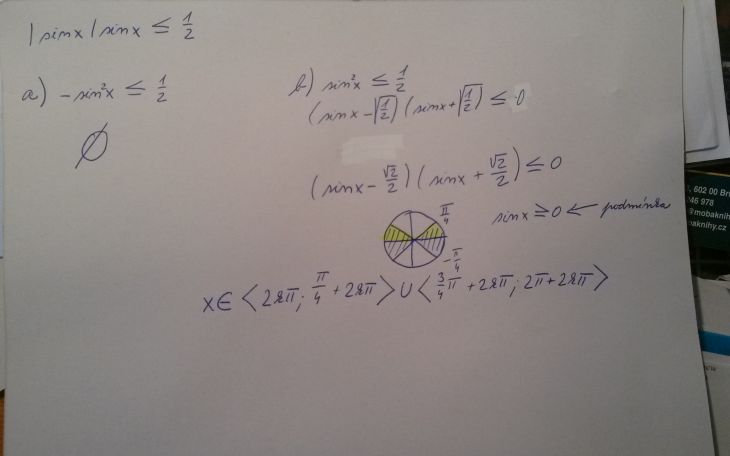Goniometrická nerovnice

Od: elisa24® 11.01.15 11:34 odpovědí: 6 změna: 11.01.15 19:13

Dobrý den, je prosím správně postup u tohoto příkladu, moc si nejsem jistá tím a), ale odmocnina ze záporného čísla udělat nejde, že? A omezení intervalu v b) - nebude záporný na jednotkové kružnici, to vychází z podmínky pro sin x nadruhou? Jinak výsledek je dobře. Děkuji

 

6 odpovědí na otázku

Řazeno dle hodnocení

 

 

kartaginec®

11.01.15 13:09

2x

Není to dobře. Případ a: vlevo máte skutečně vždý záporné, přesněji nekladné) číslo, takže řešení nerovnosti

– sin² x ≤ ½

není Ø, ale R.

( k tomu samozřejmě musíte ještě zohlednit opodmínku |sin x| = – sin x.)

elisa24®

11.01.15 13:19

Jak se zohlední ta podmínka? Z a) bude řešení celé R?

kartaginec®

11.01.15 14:35

Ta podmínka |sin x| = – sin x je vlastně podmínká sin x ≤ 0, čili nerovnost a) sice platí pro celé R, ale my ji řešíme pouze pro intervaly + 2kπ, k celé, nebo chcete-li. pro UkεZ (tím symbolem UkεZ myslím sjednocení příslušných intervalú přes všechna celá k; nenašel jsem v nabídce editoru takové epsilon, co se používá pro označení "být prvkeM". Druhá možnost je použít znak eura €, který je trochu podobný¨. Ostatně takto jste pojednala i ten případ b).

elisa24®

11.01.15 17:25

Jak na tu podmínku prosím přijdu?

kartaginec®

11.01.15 17:51

To se mi zdálo, že víte, když analogickou podmínku uvažujete v případě b). Jde o to, že |sin x| = sin x, pokud sin x≥0 a v tom případě je sin x |sin x| = sin² x , což je váš případ b), a pokud je sin x ≤ 0, je |sin x| = – sin x, sin x |sin x| = – sin² x a to je pak případ a). (Případ sin x = 0 spadá pod oba tyto případy, protože +0 = –0.)

elisa24®

11.01.15 19:13

Mockrát děkuji

Skočit na otázku
Vložit novou otázku

[přidat komentář]

 

Přidat svou odpověď

 

Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.

Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.