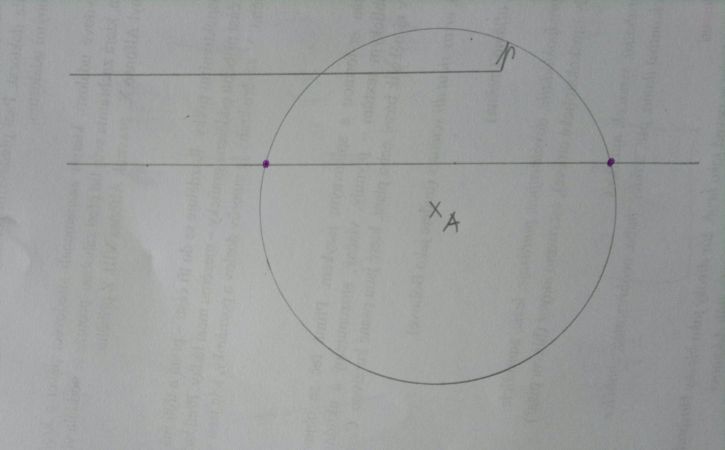
Je daná přímka p a bod A který na ní neleží. Sestrojte množinu bodů, které mají všechny od bodu A vzdálenost 4 a od přímky p vzdálenost 2cm.
Nevíte a jakou množinu se jedná?
Děkuji moc!
2x
Jen pro zajímavost, dříve se takové množině říkalo geometrické místo (bodů s danou vlastností).
A k počtu řešení: je-li vzdálenost d bodu A od přímky p byla větší než 6, úloha by neměla žádné řešení (přesněji řečeno, tato úloha má vždy řešení, ale v tomto případě je řešením množina prázdná). Pro d = 6 je tato množina jednobodová a ve všech ostatních případech (včetně vyloučeného případu, kdy bod A leží na p) je dvoubodová.
doplněno 12.01.15 09:20:Oprava: pro d větší než 6 je řešením prázdná množida, pro d =6 jednobodová, pro d mezi 6 a 2 je dvoubodová. pro d=2 tříbodová a pro zbytek čtyřbodová.
Omlouvám se, nenakreslil jsem si to a jednu chvíli jsem zaměnil poloměr kružnice za průměr (i když je to pitomost).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.