Ahoj, poradíte mi prosím někdo s tímto příkladem? Nevím si s ním rady z toho důvodu, že při řešení musím použít otočení.
Planimetrie, 3.48
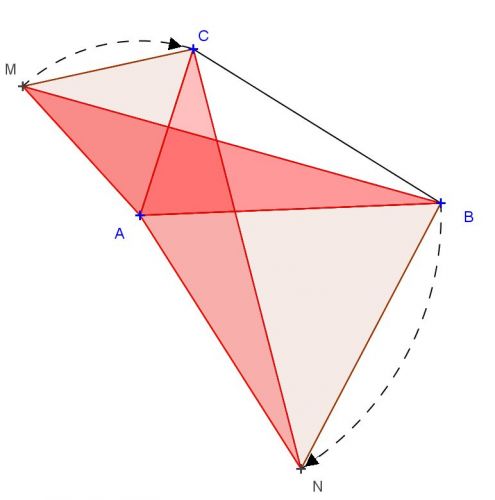
Je dán ostroúhlý trojúhelník ABC. Nad jeho stranami AC a AB jsou sestrojeny vně trojúhelníku ABC rovnostranné trojúhelníky ACM a ANB. Dokažte, že se délka BM a CN rovná.
2x
Ahoj, za daných podmínek trojúhelníky MAB a CAN jsou shodné. Jeden je otočením druhého podle středu A o úhel α původního trojúhelníku ABC. Shodnost trojúhelníků plyne ze shodnosti dvou stran a jednoho úhlu, konkrétně MA = CA a AB = AN a úhlů MAB = CAB, které jsou oba o 60°větší než původní α.
doplněno 09.01.15 00:40:Ano, x má pravdu. Je to tak.
Dovolil bych si řešení trochu upřesnit. Doopravdy se jedná o otočení (rotaci) se středem v bodě A, ale o úhel 60°, nikoli o úhel α. Jelikož otočení patří mezi shodná zobrazení, pak i trojúhelníky AMB a ACN jsou shodné, proto |CN| = |MB|.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.