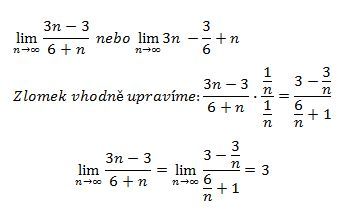Zdravím, všechny potřeboval bych poradit s postupem při řešení následujících limit posloupností. Bohužel jsem nikde v sešitě ani v učebnici nenašel vzorový příklad na tyto limity ( s jinými čísly), takže nevím, jak postupovat, i když základy trochu vím (ale u jiných typů příkladů na limity). Díky předem za ochotu, příklady jsou následující:
lim (n až nekonečno) 3n-3/6+n
lim(n až nekonečno) 3n-3/2n+3n
lim(p až nekonečno) p2-3/q+1
lim(q až nekonečno) 2p-2q
1x
Předně trochu si upravte jednořádkový zápis lomených výrazů, čitetel i jmenovatel musí být v závorce, protože jinak by měl příklad jiný smysl.
Například váš zápis 3n-3/6+n by se neřešil jako (3n-3)/(6+n), ale řešil by se jako 3n - (3/6) + n, tedy 4n - (3/6), což je 4n - (1/2), protože dělení má přednost před sčítáním a odečítáním. Ale to je vedlejší, vaše příklady jsou pochopitelné.
Podívejte se na docela pěkný výklad i s řešenými příklady na matematika.cz/...
děkuji, po úpravě se tedy jedná o tyto příklady:
lim (n až nekonečno) 3n-3/6+n
lim(n až nekonečno) 3n-3/2n+3n
lim(p až nekonečno) p2-3/q+1
lim(q až nekonečno) (2p-2q) - podle zadání je v závorce jenom poslední příklad, zbytek je normálně tak, jak jsem napsal, bez závorky (nebo že by na ni zapomněli) poznámka, n, p, q jsou přirozená čísla
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.