zdravím, mám následující příklady a výsledky, které mi vyšly, přikládám. U některých příkladů si nejsem příliš jist postupem, tak prosím kdyžtak o doplnění.
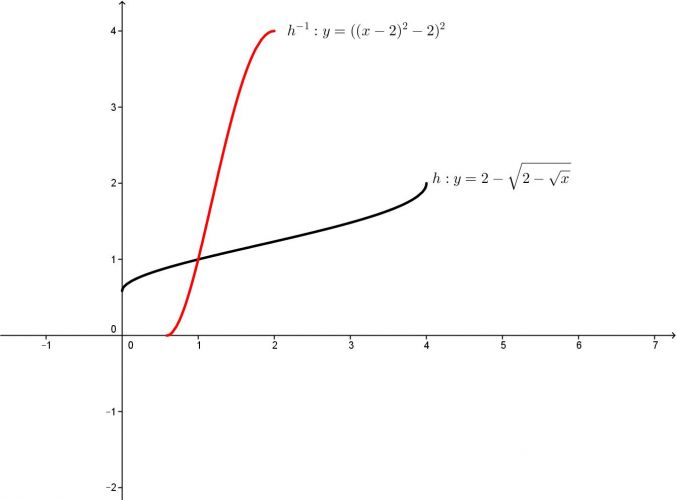
funkce h: y = 2-pod druhou odmocninou je 2 minus další druhá odmocnina(tato odmocnina je ještě pod předešlou odmocninou) a pod touto odmocninou je x. Mám vypočítat h-1 (21). Můj postup - napřed prohození x za y, ale dále nevím (respektive nevím, jak odstranit ty odmocniny s tou neznámou)
(omlouvám se, nevím, jak zde vypadá odmocnina, jinak bych psal rovnou s ní, ale ani ve speciálních znacích nic nevidím.![]() )
)
Další příklad:
f(x) = 3x + 7
g(x)= ln(druhou odmocnina, pod kterou je "x", konec odmocniny a dále minus 3)
vypočítejte hodnotu g(f(2)) a f(f(2))
moje výsledky: pro g(f(2)) -3(3x2+7)=-39
pro f(f(2)) = 7-(3x2+7)=-6
Poslední příklad: určete definiční obory funkcí
f(x) =2/6x - můj výsledek: R-(0) nebo možná (0, + nekonečno)
g(x)= pod druhou odmocninou(vše je pod odmocninou) je x2-4
můj výsledek: (-nekonečno,-2) U <2,+nekonečno)
h(x) = ln(3-x) + ln(4-x)
můj výsledek: (-nekonečno,3> U <4, + nekonečno)
Děkuji mockrát, snad je srozumitelné.
4x
Dobrý den,
rádi pomáháme, ale cílem poradny je, aby se to žáci sami naučili, nikoliv abychom tu za ně vytvářeli hodiny a hodiny nudné domácí úlohy, kdy nám tu napíší zadání a výsledek z výsledků v učebnici vzadu, kolik má vyjít a pak to jen opsali. Jistě to není váš případ, pokud píšete, že si jen nejste jist postupem. Prosím tedy, doplňte váš postup u výpočtu. Pokud bude chybný, rádi opravíme. Pokud se dostanete do úzkých, posuneme vás. Díky za pochopení.
doplněno 02.01.15 14:45:Postupy, které uvádíte pro poslední příklad na definiční obory, jsou správně, jen řešení x pro 4-x větší než 0 není x větší než4, ale xmenší než4, takže výsledný průnik bude jinak. Postup pro 1. příklad obecně je soustředit odmocniny na jedné straně rovnosti (v 1. kroku tady není potřeba), umocnit a toto opakovat tak dlouho, dokud nejsou všechny odmocniny vyřešeny.
Postupy pro řešení složených funkcí jsou úplně vedle.
f(f(2)) = 3(3*2+7)+7 = 46
obdobně
g(f(2)) = ln(odmocnina(3*2+7)-3) = atd.
doplněno 02.01.15 14:57:Inverzní funkce z 1. příkladu, striktně vzato, bude mít definiční obor takový, jaký má první funkce obor hodnot, což je uzavřený interval 0 až 2 odmocniny ze 2. Tam 21 nepatří, takže inverzní funkce nemá v bodě 21 hodnotu.
doplněno 02.01.15 16:16:U složené fce g(f(2)) ještě chybí udělat ten logaritmus (vyjde cca -0,5). U 1. příkladu se mi sice vloudila chybka, obor hodnot původní funkce je 2-odmocnina dvou až dva, ale ani tam hodnota 21 nepatří. Chybka tedy asi bude v tom, že zápis h-1 (21) znamená něco jiného, než hodnota inverzní fce v bodě 21, případně ještě převyprávění vzorečků se nějak nepodařilo a špatně jsem to pochopila.
Díky za upozornění, rozepíšu ještě u některých příkladů postup, to není problém. Správné výsledky k dispozici nemám (ani je za správné nepokládám).
postup u definičních oborů:
2/6x - podmínka x ≠O, dále celý výraz>0
pod odmocninou x2-4, stejný postup, položím výraz>0 , pak převedu x2 a odmocním
ln(3-x) + ln(4-x), stejný postup, položím výraz>0, vypočtu x
postup u výpočtu hodnoty funkcí (příklad 2)
7 - (3x + 7) => pro x=2 dosadíme za x 7-(3x2+7)=-6
pro druhou hodnotu: 3x(3x2+7)= 39
Tak jsem dopočítal ten druhý příklad, jak jste mi poradil, tedy:g(f(2)) = ln(odmocnina(3*2+7)-3) = což je tedy odmocnina ze 13, což je 3,61 po zaokrouhlení, minus 3, mi tedy vychází 0,61 po zaokrouhlení.
Pracuji a zadávám výsledky přes PC, má se zaokrouhlovat na dvě des. místa, takže by to mělo být v pořádku, ale není.
Ostatně tedy ten první příklad je podle vás nejde definovat, takže jsem to tak napsal, ale to je také špatně. Nevím, asi nějaká chyba při zadávání výsledků učitelem...zkusím to asi probrat ve škole.
Teď se jdu podívat ještě na ten první příklad.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.