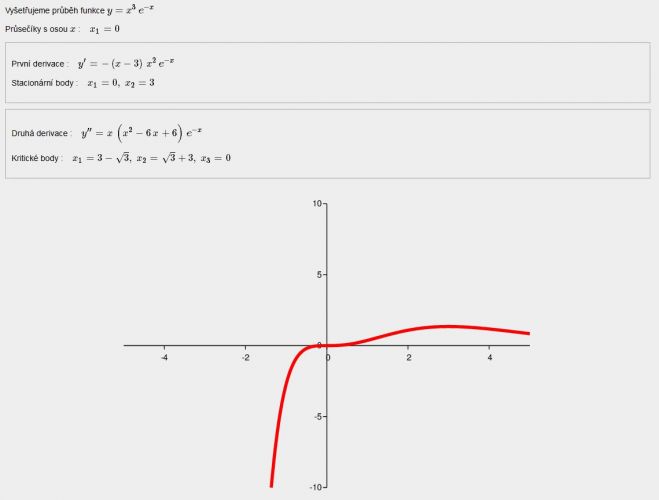
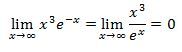Dobrý den, mám zadanou funkci: x^3*e^-x. Mám vypracovat průběh funkce. Něco mám, ale nevím si rady s tím, jak zlimitovat (x jdoucí k nekonečnu) a jak najít inflexní body a asymptoty. Děkuji.
2x
Děkuji za inflexní body, je mi to jasné (graf mám stejný, tak jsem si to alespoň zkontrolovala). Co se týče limity, tak si nemyslím, že když mám součin, mohu z toho udělat podíl a poté derivovat. Ale zase nevím, jak na to jinak. Ještě mi tedy do průběhu funkce chybí ta limita.
Jak praví @x, ta funkce je ve tvaru podílu, žádný podíl ze součinu dělat nemusíte. Na druhou stranu, vždy můžete ze součinu udělat podíl pomocí složených zlomků, například A*B = A/(1/B); otázka je, kdy je to výhodné.
No a pro úplnost , když jsem výše tvrdil, že to jde různě a vy nevíte, jak na to jinak, poradím vám aspoň jednu cestu, pokud ovšem znáte Taylorovy řady. Pokud ex rozvinete do Taylora, z rozvoje ihned vidíte, že pro kladné x a pro libovolné n přirozené platí ex> xn/n!
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.