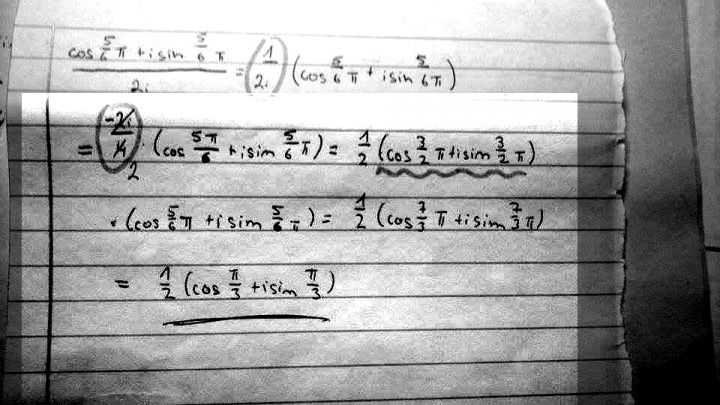Ahoj, potřebovala bych vysvětlit vše, co je zeleně zvýrazněno. Respektive nechápu, jak z 1/2i dostaneme -2i/4 a jaktože si může následně dovolit zkrát "i"na 1/2. Kam to "i"zmizelo? Plus pak nechápu, kde vzal závorku s (cos 3/2 pí + i sin 3/2 pí).
Děkuji za vysvětlení, zbytek je mi už jasný. ![]()
Příklad zde: fbcdn-sphotos-h-a.akamaih/...
2x
Z definice i plyne, že 1/i=-i.
Z toho je tím pádem jasné, že 1/2i=-i/2.
Cos(3/2π ) + i*sin(3/2π )=0+i*(-1) je šikovné dosazení za –i, které se dalšími úpravami dá promítnout do změny argumentů cosinu a sinu.
doplněno 14.12.14 15:41:Ten člověk to udělal proto, aby se zbavil i ve jmenovateli, což se obecně udělá rozšířením zlomku číslem komplexně sdruženým ke jmenovateli, v tomto případě -2i.
Dosazování za i se můžete vyhnout, s tím, že i roznásobíte následující závorku, dostanete -sin...+icos... a budete následně přemýšlet, jaký argument použít tak, aby se závorka dostala do standardního tvaru cos...+isin...
doplněno 14.12.14 16:04:Kartagiňče, to nevadí, třeba zrovna to vaše podání tázající lépe pochopí. Jste velice obětavý člověk, moc si vás osobně vážím za to, jak tu pomáháte dětem s učením. ![]()
Tak definici 1/i = -i chápu, spíše jsem nepochopila, proč tam cpal ty čtvrtiny, které následně zkrátil na tu jednu polovinu. Přijde mi to jako naprosto zbytečný a matoucí krok.
Tu závorku tedy už plus mínus chápu, ale stejně by mě to v písemce nenapadlo, abych ještě musela hledat nějaké dosazování za -i. Hádám, že asi není jiný krok, jak bych se tomuto vyhnula.. Každopádně děkuji za vysvětlení.
2x
Nejprve k tomu zbytečnému krácení: to je opravdu trochu nešikovná a vzniklo to patrně tak, že autor řešení pohužil standardního postupu usmšrnění zlomku: jestliže ve jmenovateli máme a + ib, rozšíříme zlomek výrazem komplexně sdruženým, tedy a – ib a do jmenovatele se dostane a2 + b2 v našem případě tedy bychom rozšiřovali výrazem –2i a tím se do jmenopvatele dostane ta čtyřka, ktyerou následně zkrátíte. Samozřejmě že trochu kritickým pohledem vidíme , že je to zbytečně komplikované. Přiznám se, že tak úplně nechápu, co je míněti tím "z definice i plyne". Samozřejmě vše konec konců vše plyne z definice, ale tady bych prostě ten zlomek rozšířil i, případně –i.)
A ten druhý problém: samozřejmě lze –i vyjádřít výše uvedeným zpúsobem – je to vlastně goniometrický tvar čísla
–i
– a pak použít Moivreovu poučku, ale mohli bych se na to podívat i z jiného úhlu: proste roznásobíme i(cos α + i sin α ) = –sin α + i cos α a následně převést sinus na cosinus a naopak pomocí vztahú mezi goniometrickými funkcemi posunutých argumentů. Ten způsom, který použil autor řešení a který vysvětlila dejavu, je elegantnější a rychlejší, ale takhlo mně to možná spíš napadne, zejména když směřuji ke goniometrickému tvaru komplexního čísla, v němž reálná složka je vyjádřena pomocí kosinu a sinus je věnován složce imaginární.
A drobný doplněk: já se svou kataraktou se ve vašem obrázku trochu obtížně orientuji a tak jsem si dovolil ho troch upravit a připojit.
No a koukám, že než jsem to doťukal, v podstatě totéž napsala i dejavu. No tak snad je k něčemu aspoň ten obrázek.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.