Nejste přihlášen/a.
Dobrý den,
v matematice teď děláme exponencialní funkce. Máme umět určit funkce, které jsou větší než než 1 atd
Vše je v příloze. Místo otazníků mají být zobáčky ( větší menší )
Tyto příklady nemáme počítat s kalulačkou a ani si příklad nemůžeme vypočítat bez kalkulačky na papír. Musíme prostě to hned říct na první pohled. Nemohl by jste mi někdo poradit?
Děkuji
0x
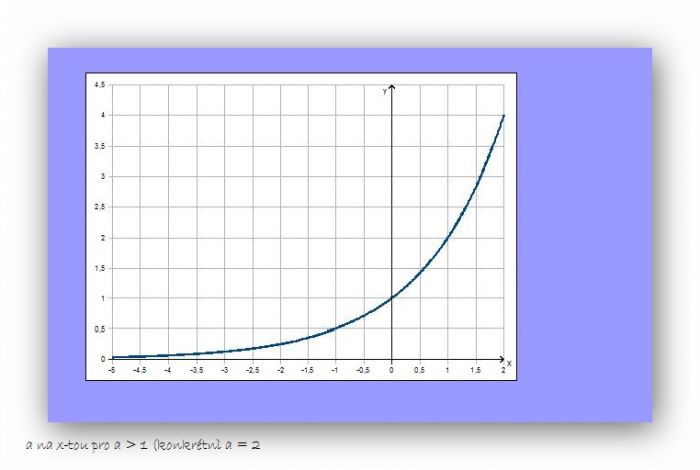
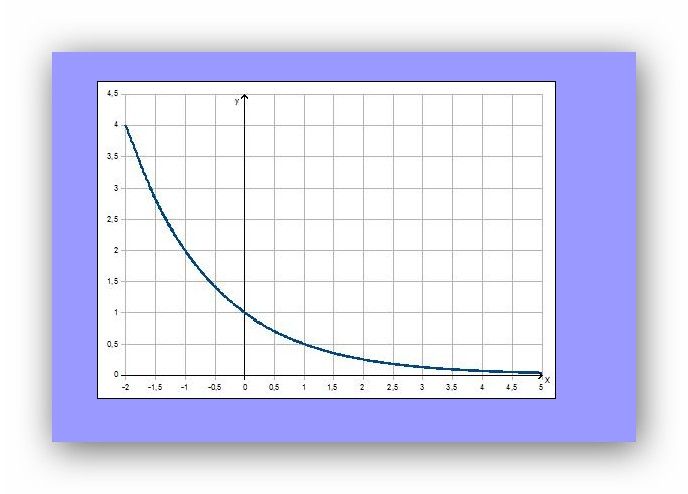
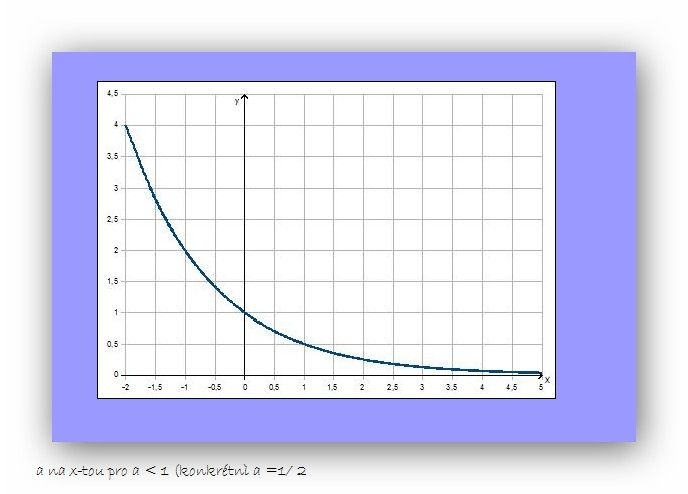
No a co už víš o exponenciálních funkcích? Určitě třeba to, že v nule (x=0) všechny procházejí jedničkou (y=1); protože cokoliv (normálního) na nultou je 1. No a exponenciála (kladného čísla) buď pořád roste (a to pořád rychleji a rychleji), nebo pořád klesá (zleva nejdřív strašně rychle a postupně brzdí, ale pořád klesá), výjimku tvoří exponenciílní funkce 1, protože 1 na cokoliv je 1, to je "vodorovná" přímka. A co je jak, na to stačí si uvědomit třeba funkci 2^x: v nule (x=0) je to 1, v jedničce (x=1) je to 2, ve dvojce 4 atd., takže to je ta rostoucí. Pro 0,5^x je v nule 1, v jedničce 0,5, ve dvojce 0,25 atd. takže to je ta klesající. Takže vidíš, že cokoliv většího, než 1 (protože ta dává přímku), má rostoucí průběh, cokoliv menšího, než 1, má klesající průběh.
Takže:
2) (41/40)^0,2 je "víc než 1 na kladný exponent", takže je to>1
4) to je jen chytáček; jak se liší pravý výraz od levého?
5) je tam "víc než 1 na něco" (takže rostoucí funkce), ale pravý výraz má zápornější exponent, než levý výraz, takže pravý výraz je v grafu "(odm(3))^x" víc vlevo, takže musí mít hodnotu ... menší, takže ">".
Logicky bych si to odvodil dle exponentů 1.2 <1,8 když to, aledam do kalkulačky, tak mi to vyjde naopak
TA kalkulačka je na kontrolu dobrá. Vtip je v tom, že tady máte základ menší než jedna a tam je ta monitonie obráceně. (Čím víc číslo menží než jedna umocňujete, tím víc se zmenšuje. 1/2 je menší nežý jena, a jedna čtvrtina tím "menšejší". To jste tu půlku znásobil něčím meněím než jedna, vlastně jste ho vydělil dvěma.
Už vím. Když je zlomek - určím si monotonnost a až pak porovnám exponenty když mám, ale tento příklad:
2 exponent odmocnina ze 2 <2 exponent odmocnina ze 3
Jak mam toto určit. Když 2 je suda tak je funkce tak funkce je rostouci?
Není důležité, zda je základ sudý či lichý (ostatně tento pojem má smysl jen pro celé základy, třeba pro důležitou funkci ex to smysl nemá), ale zda je menší či větší než jedna (samozřejmě kladný musí být vždy). pro základ a = 1 je funkce ax konstantní (vždy rovná jednéú a jednička tvoří předěl. Je-li a <1, je ax klesající a pro a> 1 je rostoucí.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
