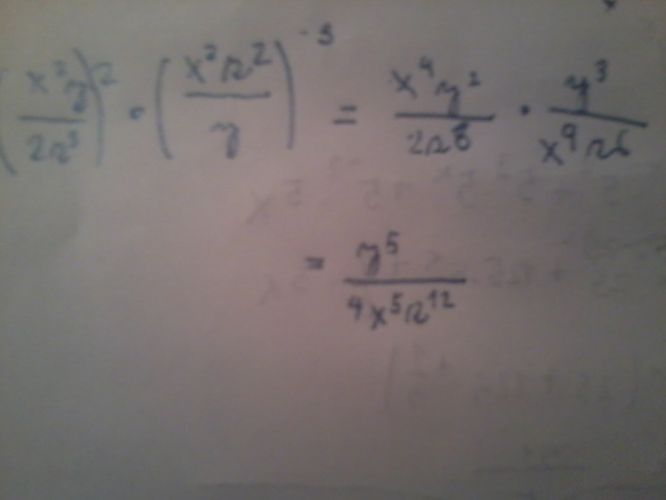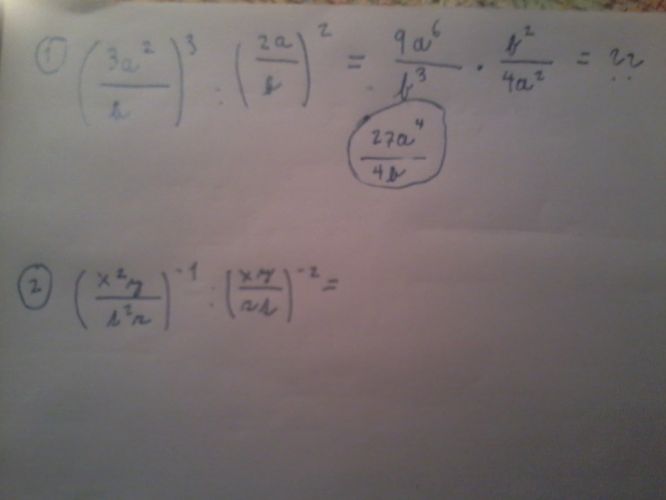Dobrý den,
potřeboval bych poradit s tímto příkladem. Vubec nevím kde dělám chybu. Mohl by mi někdo napsat postup?
Děkuji ( dole je výsledek )
doplněno 09.12.14 18:03:Nikde dělám pořád nějako chybu
U toho posledního příkladu : když mám -1 zlomek se musí otočit, ale když tam mám děleno, tak se zase otočí - takže ve výsledku se otáčet nebude?
0x
Na prvním obrázku, kdo dělal ty úpravy? V prvním zlomku jmenovatel je (2*z^3)^2 a to se rovná 4*z^6, ne 2*z^6.
Druhý obr. druhý příklad: mocnina -1 platí jen pro první zlomek (takže ten se převrátí), mocnina -2 platí jen pro druhý zlomek (takže ten se převrátí), ani jedna operace se netýká prostředního "děleno". Je tam vlastně A:B, jestli si nějak upravíš nebo zjednodušíš A, či B, nic to nemění na "velkém" zlomku A:B. Ale je pravda, že A:B můžeš napsat jako A*(B^-1), takže to výsledné nepřevrácení se bude týkat zlomku B (když je "na -2"). Já si vždycky radši napíšu složený zlomek už bez záporných mocnitelů a pak násobím "vnější členy " a dám nahoru a potom násobím "vnitřní" a dám dolů {(a/b) / (c/d)=ad/bc}, je to možná o krok víc, ale aspoň se mi to převracení a mínusy nepopletou.
Druhý obr. první příklad: 3^3 není 9.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.