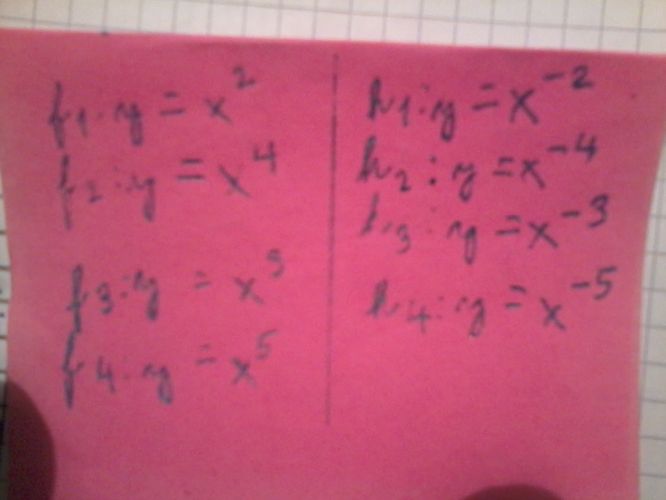Mám narýsovat graf. Abych ho narýsovala musím udělat tabulku. V tabulce již byl zadaný první řádek ( -2;-1;-0,5;0; 0,5; 1; 2 ) dál mám daný predpisy. Vůbec nevím jak to mám dál udělat
2x
Vždyť už něco dalšího doplněno máš (ale blbě).
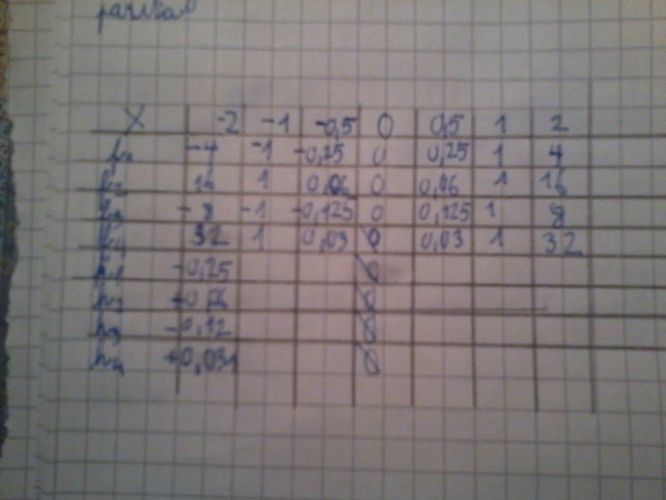
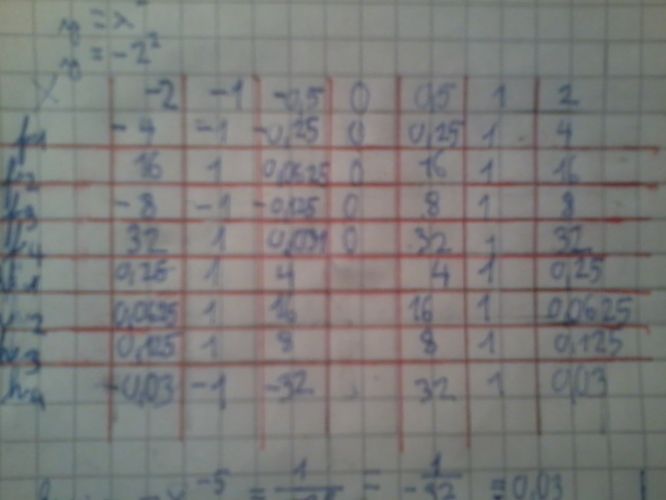
První řádek patrně udává hodnoty X, pro které si máš spočítat hodnoty Y jednotlivých funkcí F1..H4. Takže když do dalšího řádku budeš chtít psát hodnoty F1, tak postupně dosadíš hodnotu X podle sloupce a výsledek (tzn. Y) zapíšeš do políčka tabulky. Tedy první hodnota funkce F1 bude pro X=-2 a bude {znakem ^ označuji mocninu} Y=X^2=(-2)^2=(-2)*(-2)=4, do prvního políčka napíšeš 4. Druhé políčko (v řádku F1) je pro X=-1: Y=X^2=(-1)^2=1, napíšeš 1. Třetí políčko pro X=-0,5: Y=X^2=(-0,5)^2=0,25, zapíšeš 0,25. Atd.
Sedmou funkcí je H3: Y=X^(-3). První políčko tohoto řádku je zas pro X=-2, takže
Y=X^(-3)=1/(X^3)=1/((-2)^3)=1/(-8)=-(1/8)=-0,125, zapíšeš -0,125. Atd.
A až budeš mít tabulku vyplněnou, nakreslíš postupně grafy pro jednotlivé funkce. To už zvládneš, ne?
doplněno 26.11.14 18:55: Nerozumim tomu prvnimu kroku.
Proč 1/(x^3)?
H? Ty záporné mocniny? Co konkrétně?
Když Y=X^(-něco), tak je to stejné, jako Y=1/(X^něco).
X^(-2)=1/(X^2); {X na -2 = 1/(x na 2)}
X^(-7)=1/(X^7); {X na -7 = 1/(x na 7)}
a obecně: X^(-A)=1/(X^A)
Takže třeba H4: Y=X^(-5) si rovnou můžem napsat jako Y=1/(X^5) a pak už jen dosazujem za X.
X=-2: Y=1/((-2)^5)=1/(-32)=-(1/32)
X=-1: Y=1/((-1)^5)=1/(-1)=-1
X=-0,5: Y=1/((-0,5)^5)=1/((-1/2)^5)=1/(-1/32)=-32; těch 0,5 jsem si převedl na zlomek, protože se s tím pak lépe počítá z hlavy, počítám pátou mocninu 2
X=0: Y=1/(0^5)=1/0 = dělení nulou a to nejde!
X=0,5=1/2: Y=1/((1/2)^5)=1/(1/32)=32; těch 0,5 jsem si zas převedl na zlomek jen pro lepší počítání
X=1: Y=1/(1^5)=1/1=1
X=2: Y=1/(2^5)=1/32
Snad jsem se nikde nespletl. Hlavně pozor na mínusy a na správný zápis do zlomků.
Tady wolframalpha.com/... se můžeš podívat, jak ten graf H4 zhruba vypadá.
doplněno 26.11.14 19:32:Taky se můžeš podívat na
cs.wikipedia.org/...
stačit budou jen ty základy, složitosti nezkoumej.
A jaké jiné číslo bych tam měl dát?
To je pravidlo, že mocniny se záporným exponentem se mohou převést na převrácenou hodnotu toho celého, ale s kladným exponentem.
Obecně: X^(-A)=X^(-1 * A) a součin v exponentu se přece dá napsat jako
(X^A)^(-1) nebo (X^-1)^A
A protože Y^(-1)=1/Y (to prostě platí), tak i ten předchozí řádek se dá napsat jako 1/(X^A) nebo (1/X)^A a obojí vede na stejný výsledek, protože umocněný celý zlomek (1/X)^A=(1^A)/(X^A) a protože platí 1^A=1, dostanem zas jenom 1/(X^A).
Uf, snad to není moc nepřehledné. Ale stačí si pamatovat, že platí Z^(-1)=1/Z {Z na -1 = 1/Z}.
doplněno 26.11.14 20:50: Nvn nemají ty H které jsou v sloupečku s -2; -1; -0,5 záporný?
Teď počítám další příklady. Abych mohl udělat graf musím si udělat tabulku. Tu jsem udělal. Mám doplněnou dobře funkce g? Jak mám udělat funkce e? Pro x -2 mi vyšlo0,1 to je asi špatne že?
Příště sem napiš (nebo radši ofoť, ať to blbě neopíšeš) své postupy. Jak jsi třeba přišel na G pro X=-1? Přece když G=(X-1)^(-4)=1/((X-1)^4) a dosadím za X tu -1, tak dostanu
G = 1 / ((-1-1)^4) = 1 / ((-2)^4) = 1/16
A třeba pro X=0 je G=1/((0-1)^4) = 1/ ((-1)^4) = 1/1 = 1
Zato pro X=1 dostanem ve jmenovateli 0 a to nejde. To jsi ty výsledky jen odhadoval?
Co ti připadá složitého na funkci E? Máš tam "X^(-3) - 1", tak tam prostě dosaď za X požadované hodnoty. Nejdřív si to třeba přepiš do toho tvaru "(1/(X^3)) - 1" a pak dosaď. A kdyby ses dobře podíval, tak E je vlastně funkce H3 zmenšená o 1, takže bys ani moc počítat nemusel. Ale radši si to nezjednodušuj a počítej.
Pozn.: Ta tvoje tabulka z 26.11 20:47 je špatně. Byla špatně hned poprvé a je špatně pořád. Třeba řádek pro F1 určitě nebude obsahovat žádnou zápornou hodnotu. Dokonce jsem ti to poprvé spočítal a ani jsi ty výsledky neopsal. Tak teď mi poraď, co s tebou?
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.