Nejste přihlášen/a.
Dobrý den,
Chodím do prvního ročníku na VUT v Brně. Bohužel na mojí předchozí škole jsem se s tímhle předmětem nesetkal, a tak v něm tak trochu plavu. Právě jsem dostal za úkol narýsovat kulovou plochu v Mongeově promítání. Jelikož netuším jak na to, tak bych Vás tady chtěl někoho požádat o radu. zadání zní:
V Mongeově promítání sestrojte kulovou plochu, jestliže její hlavní kružnice k (kružnice k má střed ve středu kulové plochy) je určena body A=[-20,10,40], B=[20,50,40], C=[0,10,60].
Doufám že se najde někdo ochotný mi poradit. Uvítám jakékoliv odpovědi, tipy, cokoliv.
Děkuji. ![]()
2x
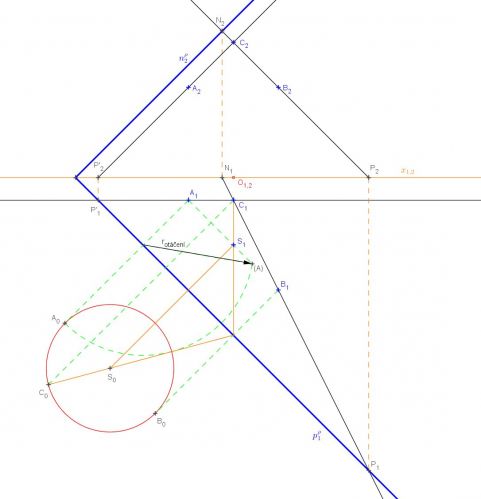
Rovinu určenou třemi body A, B, C otočíme do průmětny. Poté můžeme sestrojit kružnici určenou body A0, B0, C0 a její střed S0. Pak střed S0 otočíme zpět a získáme tak průměty středu. Při tom lze využít pravoúhlou osovou afinitu, jejíž osou je stopa roviny ABC.
Děkuji za radu. Od toho se snad budu moct nějak odrazit. Nemohl/a byste mi to třeba aspoň tak trochu názorně načrtnout aspoň začátek? Moc by mi to pomohlo. Děkuji ![]()
Pomocí přímek AC a BC jsem sestrojil stopy roviny ρ = ABC. Poté jsem body A, B, C otočil kolem půdorysné stopy do půdorysny – body A0, B0, C0. Nejprve jsem otočil bod A a body B0, C0 jsem sestrojil pomocí pravoúhlé afinity. Poloměr otáčení jsem zjistil sklopením bodu A do půdorysny – bod (A). Pak lze sestrojit střed kružnice S0 jako průsečík os úseček A0C0 a B0C0. Pomocí afinity sestrojíme S1 – průmět středu kulové plochy-
Děkuji Vám mnohokrát. Stále mi není jasné jak přesně mám zjistit R otáčení (bod (A)) a následně jak sestrojit body A0 B0 C0. Nevěděl by mi to někdo jednoduše vysvětlit? ![]()
Bod A0 leží na kolmici ke stopě spuštěné z bodu A1. (A) je sklopený bod A do půdorysny. Vzdálenost (A)A1 je rovna souřadnici zet bodu A (v našem případě z = 40). Poloměr otáčení bodu A je vyznačen na obrázku.
Doporučuji si stáhnout mdg.vsb.cz/...
Na stránce 45 a dále je popis otáčení roviny.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.