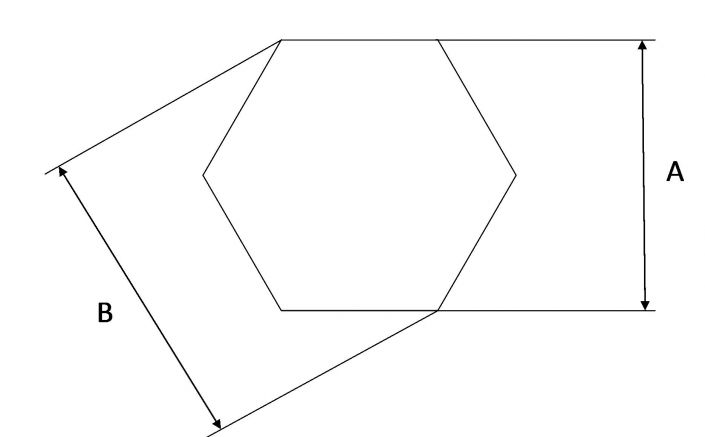
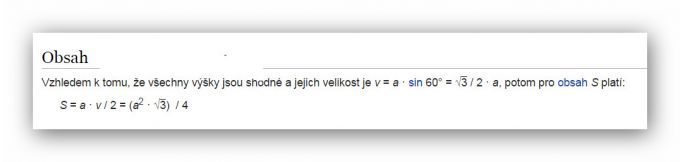
Mám pravoúhlý trojboký hranol a znám výšku, ta je 11cm a součin strany C a B pravoúhlého trojúhelníku (podstavy), která je 80 cm. Neumím vypočítat stranu A pravoúhlého trojúhelníku, neumíte prosím někdo poradit? Zkoušela jsem odvodit podle vzorců, ale pořád se v tom motám a nevím, co mám vlastně použít...
Děkuji!
0x
Prosím pěkně, zkontrolujte zadání. Za prvé, čeho znáte výšku? Pokud výšku toho hranolu, tak ta vám k ničemu není s podstavovým trojúhelníkěm nijak nesouvisí. Dále, strany mají rozměr délek a jejich součin nemůže být dán v ventimetrech, jedině v cm2 nepo obecně v nějaké plošné míře. A taky nevím, která strana jzákladny je přepona. Obvykle se označuje písmenem cé, ale běžně používáme malá písmena. Samozřejmě to je jen dohoda a můžete si ji změnit, ale když měníte dohotu v tomto bodě, nemohu se na ni spolehnout ani v jiných bodech.
A taky termín "pravoúhlý trojboký hranol" není zrovna běžný; máte na mysli "Trojboký hranol, jehož podstavou je pravoúhlý trojúhelník "?
Až se domluvíme, co je co, můžeme se bavit o řešení.
Jedná se o výšku hranolu, která je opravdu asi k ničemu...To je těch 11 cm.
b x c=80, odvěsna x přepona, máte pravdu, v zadání je jen 80 a není napsáno čeho, jestli v tom není ten fígl...
A ano, mám na mysli trojboký hranol, jehož podstavou je pravoúhlý trojúhelník, jen se neumím tak přesně matematicky vyjadřovat...
Takže děkuji za upřesnění, ale omlouvám se, asi neporadím. Řešíte trojůhelník, v němž máte dány dva údaje (součin dvou stran a pravý úhel) a to je obecně málo. Nevím, jestli není zde nějaký trik, budu ještě přemýšlet, ale nedovedu si představit, jaký. Určitě tam nemáte zadáno ještě něco implicitně? Nevznikla tato ůloha z něčeho jiného? Mate mne, že se tváří jako planimetrická úloha a přitom se tam mluví o trojrozměrném tělese.
Tak to nevím, přišel s tím kamarád, občas nás doma zásobuje takovýma hříčkama... jestli to vzniklo z něčeho netuším, ale zkusím zjistit upřesnění a případně dodám ![]()
Máme pravidelný 6-úhelník, známe následují vztah a údaje:
A x B = 80 cm
v (výška) = 11 cm
s =? {cm} (obsah), V =?
Nevím, proč z toho vznikl trojúhelník. Názorně je to na přiloženém obrázku, já jsem to zkoušela, ale toto nevím, tím, že neznám stranu a, neumím nic vypočítat...
Tak jí se pokusím o přesnější zadání, jak si myslím, že to bylo myšleno. Jen jsem s dovolením změnil některá označení, aby to odpovídalo úzu, a některá jsem doplnil, kvůli tomu, aby bylo jasno, o čem je řeč.
Takže:
Je dán pravidelný šestiúhelník a v něm zvolím tři body A,B,C podle obrázku. (Poznámka: vrcholy šestiúhelníku se obvykle označují v jiném pořadí... A,B,C,D,E,F "kolem dokola"; moje volba směřuje k pravoúhlému trojúhelníku, se kterým budeme dále pracovat.) Označme a = |BC| , b = |AC|, c = |AB| strany pravoúhlého trojůhelníka ABC s pravým úhlem u vrcholu C. (Strany se označují malými písmeny spíše než velkými, která bývají vyhrazena pro body, a navíc jsem změnil B za c, kterým obvykle označujeme přeponu, takže mnou užité označení odpovídá vašemu původnímu takto: a ≈A, b je zavedeno nově a c ≈ B) Pro tyto veličiny platí vztah a*c = 80[cm²] .(Pozor, a,c jsou délky, tedy centimetry, takže jejich součin musí být v čtverečních centimetrech, v tom je původní zadání chybné.)
Vyšetřujme dále trojbokýhranol se základnou ABC a s výškou v = 11[cm]. Spočtěte obsah S podstavy ABC v čtverečních centimetrech a objem V zkoumaného hranolu v centimetrech kubických.
{S = 40cm², V = 440cm³}
doplněno 26.11.14 12:52: Oprava: {S = 20cm², V = 220cm³}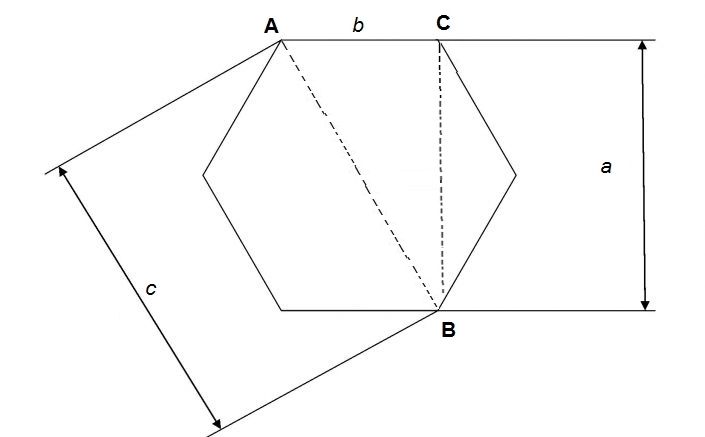
Děkuji za vysvětlení, já bych na to teda nepřišla. Jen pro zajímavost, obsah té podstavy šestiúhelníkové se dá z těchto údajů taky vypočítat? Já jsem se do toho "namočila" a teď nad tím dumám a počítám ![]() Ale zase jsem se zamotala, takové příklady mi vůbec nejdou...
Ale zase jsem se zamotala, takové příklady mi vůbec nejdou...
Ano, dá, návod podal hranolek. Prostě jakmile vypočtete jeden údaj, vypočtete všechny. Jen se to může lišit obtížností, i když jeden velký matematik dělil úlohu na neřešené a triviální; úloha jednou vyřešená přechází do kategorie triviálních.
Já jsem asi mimoň, ale já tu stranu neumím vypočítat. Vycházejí mi šílené čísla a nic pořádného...
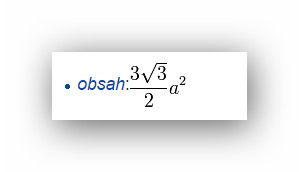
Mockrát děkuji, ten rozbor je dokonalý ![]() Ted už vše chápu a zjišťuji, že matematika je vlastně moc hezká!
Ted už vše chápu a zjišťuji, že matematika je vlastně moc hezká!
Tak to mne těší.
Ještě na závěr přidám obecnou poznámku: při podobných výpočtech se doporučuje ponechávat například odmocniny v symbolickém tvaru do posledního okamžiku. Konec konců číselný výsledek potřebujem ve skutečnosti až třeba k tomu, abychom mohli obrazaec narýsovat, případnou součástku sestrojit a tak. Poku vyčáslím předčasně, za prvé okamžitě dochází k zaokrouhlovacím chybám, dále správnost toho číselného výsledku se těžko kontroluje, no a právě díky těm zaokrouhlovacím chybám každá případná další úprava může vycházet čím dál tím hůře.
Tohle už je něco jiného.
en trojúhelník, o kterém šla řeč v minulém zadání, je asi trojúhelník, jehož jedna strana je strana šestiúhelníka, (zatím neznámá), druhá strana je jeho hlavní úhlopříčka (rovná B) a třetí strana je rovna A a je to vedlejší úhlopříčka. Kolega se zřejmě snažil vytáhnout to podstatyné, ale ztratil při tom důležitou informaci: ten trojůhelník není libovolný, vznikl z pravidelného šestiúhekníku a speciálně z toho plyne, že B ´2a. Takže teď už máte dost informací, v podstatě k určení strany a musí stačit jediný údaj, neboť všechny pravidelné šestiúhelníky jsou podobné.
Zkuste to na základě tohoto poznatku, já už jdu spat.
doplněno 26.11.14 09:55:Jen dosám, že i tato formulace je trochu nejasná, (co je s? co je V?, nesouhlasí rozměry) ale domnívám se, že v kombinaci se vstupním zadáním, kde se mluví o pravoúhlém trojúhelníku a trojbokém jehlanu, ji dokážu zrekonstruovat. A pokud se nemýlím, je ta úloha ještě jednodušší, než si myslí hranolek ; strany trojúhelníka vůbec počítat nemusíte a úlohu lze vyřešit zpaměti. Zkuste to, já jdu snídat, a když, tak se ozvěte.
Katastrofální zadání a při tom tak jednoduché.
Plocha 6úhelniku je plocha 6. rovnostranných trojúhelníků o straně B/2 a výšce A/2
A x B = 80
A/2 = 0.866 B/2
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.