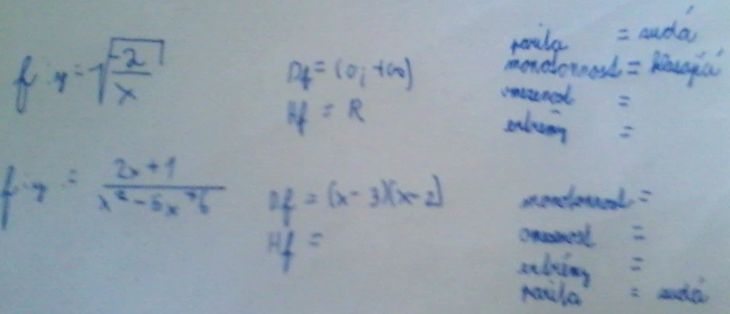Nejste přihlášen/a.
0x
Už si to moc nepamatuji, ale když si nakreslíš graf dané funkce tak bys z toho měl určit tuším D a H
extrémy se tuším dělají podle derivací a dál teď nevím
snad nevadí odkazy
zkus použít - wolframalpha.com/ dá se v něm dělat spousta zajímavých věcí a ne jen matematické ![]()

0x
No tak v grafu e to nejlépe názorně vidět. Ten graf ovšem, to je grafické znázornění věcí, které bychom měli zjistit jinak, tomu se říká vyšetřování prúběhů funkce.
Zkusil bych to na té první funkci, tedy odmocnina ze zlomku –2/x. Začal bych definičním oborem paritou, případně periodicitou, do tohohle souboru vlastností by patřil i obor hodnot a omezenost, ale ty často jsme schopni zjistit až později. Definiční obor je jasný:ve jmenovateli nesmí být nula a výraz pod odmocninou musí být nezáporný. Tedy x musí být nekladné a musí být různě od nuly; závěr:
Df = (–infty, 0)
Obor hodnot zde zjistíme snadno, ale rozhodně to není celé R, odmocnina je vždy kladná nebo nula. Ale pro každé y kladné snadno, umocněním, vypočtu y² = –2/x, x = –½ 2/y², a závěr
Hf = (0,+infty)
Zatím to odkliknu, vrátím se k tomu po obědě, ty zatím zku se zamyslet.
Pokračuji: do výsledků, týkajícich se hodnot, patří ještě: spojitost – funkce je spojitá na Df, a dále limitu v případných bodech nespojitosti (takových zde není) a v krajních bodech definičního oboru (nevím, jestli po vás vyžadují všechny tyto věci, snažím se o úplné vyšet ření průběhu): limita v nule zleva je rovna nekonečnu, limita v minus nekonečnu je nula (mimochodem, kdybychom už nevěděli, jaký je obor hodnot, odsud by nám to taky vyplynulo). Dále je funkce zdola omezená (nulou). shora je neomezená, není sudá. lichá ani periodismá.
No a teď bych přešel na ty jevy, které souvisejí s první derivací (i když ji ne vždy potřebujeme využívat), totiž monotonii a extrémy. Tohle je právě pípad, kdy bychom derivaci vůbec nepotřebovali, víme, že funkce 1/x je klesající na (–infty, 0) i na (0, + infty) – ale ne na jejích sjednocení – a odmocnina je rostoucí pro x kladné, a z toho bychom nakonec dospěli k závěru, že funkce f je na Df rostoucí, ale ve složitějších případech bychom funkci f zderivovali a zkoumali znaménko derivace, v intervalech, kde je derivace kladná, je funkce rostoucí, tam, kde je záporná, je klesající, a tam, kde je rovna nule (nebo neexistuje), může, ale nemusí být extrém – lokální či globální. Zda tam je lokální extrém, to nám pomůže zjistit druhá derivace, ale když už počítáme první derivaci všude a známe intervaly monotonie, snáze to zjistíme z těchto údajů. V našem případě je derivace stále kladná (spočtěte si ji, uníte to?), funkce je na Df rostoucí a protože Df je otevřený interval, nemá extrémy (ale samozřejmě má infimim pro x jdoucí do méně nekonečna a (nevlastní) supremum pro x jdouci k nule zleva.
V další fázi bychom počítali druhou derivaci a zjišťovali konvexnost/konkávnost, ale bnecidím že to by byl pojem, na který se ptáte, tak o něm nebudu mlivit,
V tom prvním příkladu není ani sudá, ani lichá. Vlastně jsem to i napsal, a obecné, aby mělo smysl vůbec o paritě uvažovat, musel by definiční obor být symetrický podle počátku, abyste do funkce mohl s každým x dosadit i –x,
Zkuste to nejdřív, já teď jdu pryč. Něco jste sem napsal, ale to jsou výstřely do prýzdna, napište. proč si to tak myslíte. Spediálně s tou sudostí se mýlíte, zkuste si si dosadit nějaké x a číslo k němu opačné. A monotonie – mně se to nezdá, ale pokud to tvrdíte, měla byste napsat, proč.
Tak jsem tady.
Popravdě, myslel jsem si, že byste se mohla zkusit pustit do řešení sama, vzor jsem vám nabídl. Snad jste to i zkoušelä, ale nějak vám to nejde, tak na to pojďme spolu.
Tak nejprve definiční obor. To, co píšete, totiž Df = (x-3)(x–2), to není žádný definiční obor, potřebujete najít množinu všech x, které jdou do funkce f dosadit. Výraz (x-3)(x–2) je rozklad jmenovatele, ten se bude hodit, ale není to množina. Tento výraz se nesmí rovnat nule, takže definiční obor je množina všech reálných x, pro která (x-3)(x–2)≠0, což lze zapsat různě, například jako sjednocení (–infty, 2)U(2,3)U(3,+infty). A odsud hned vidíte, že funkce není ani lichá, ani sudá. Říkal jsem vám, že aby mělo vůbec smysl o paritě uvažovat, musel by definiční obor být symetrický,Vyloučili jsme x =2 a tak by muselo být vyloučeno též x = –2, například. Ale pohovořím obecněji: prototypem sudé funkce je polynom, který obsahuje jen sudé mocniny, a u liché funkce jen kliché mocniny; odtud ten název. Tady sice máte ne polynom, ale podíl polynomů, ale stejně by musel čitatel být buď sudý nebo lichý a taktéž jmenovatel. čili, jakmile se ať v čitateli, tak ve jmenovateli střídají sudé a liché mocniny x, parita nepřichází v úvahu. Takže, v ručně psaném textu je Df špatně, v poslední otázce jste Df napsala s otazníkem, odpověď jsem napsal. paritu máte špatně. Obor hodnot... tohle je právě ten případ, kdy se k nšmu dostaneme později, měli bychom ješte zjistit limity v podech nespojitosti (takové tu nejsou) a v krajních bodech def. oboru. V obou nekonečnech je limita rovna nule, v bodech 2 a 3 existují jen jednostranné limity, v bodě 2 zleva je to plus nekonečno, stejně tak v bodě 3 zprava, kdežto v bodě 2 zprava a v bodě 3 zleva je to minus nekonečno. Odsud také hned vidíte, že funkce je neomezená, a už se rýsuje tvrzení, že obor hodnot je celé R, když tedy to f(x) se pohybuje od mínus nekonečna do plus nekonečna, ale ještě to není úplně jasné, (co když třeba neobsahuje nulu, například?).
Nejvyšší čas text odeslat, než se omylem ztratí, a pokračovat příště. Nicméně zkuste jít dál zatím sama, než se ozvu. (Zkuste třeba najít nulové body a množiny, kde je f kladná a kde záporná, to takypatří k průběhu funkce a m§že se to hodit i dále.)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.