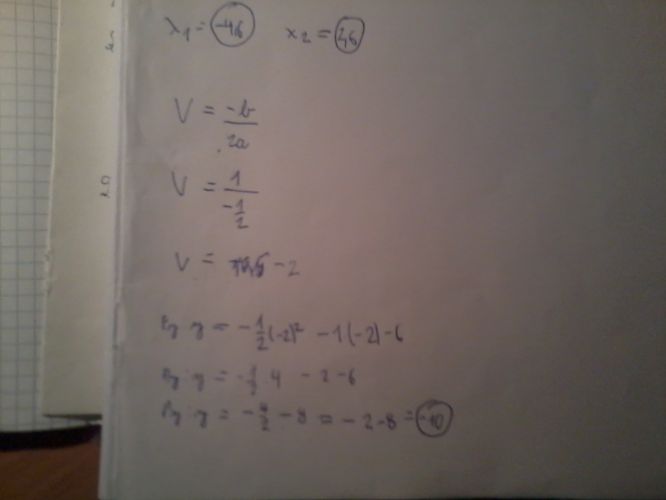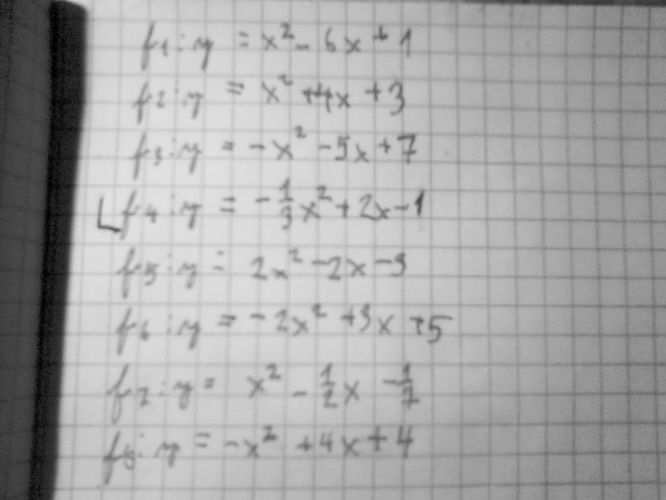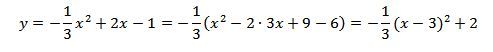Dobrý den, jsem nachlazený a tak nechodím do školy. Kámoši mi vždycky posílají výpisky atd.
Už jsem se doučil doplnění na čtverec a vypočítat diskriminant umím.
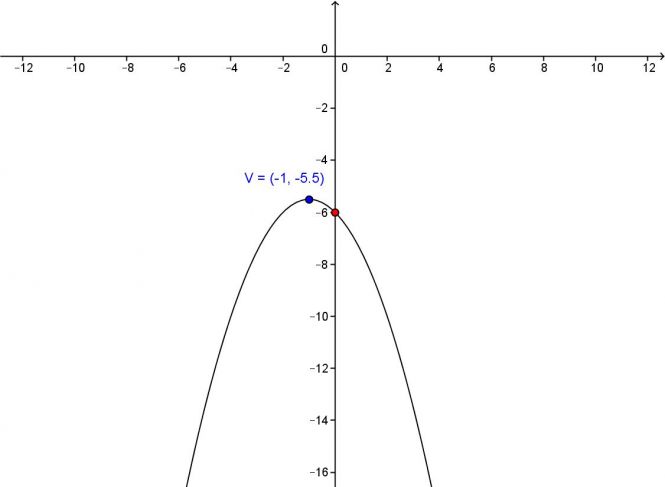
V příloze zasílám příklady, který jsou na procviční. Má se tady udělat graf. Vůbec nevím jak na to. Jak mám určit třeba V = vrchol?
Nemohly by jste mi u jakýkoliv dvou příkladu s obrázu ukázat postup? Prosím?
3x
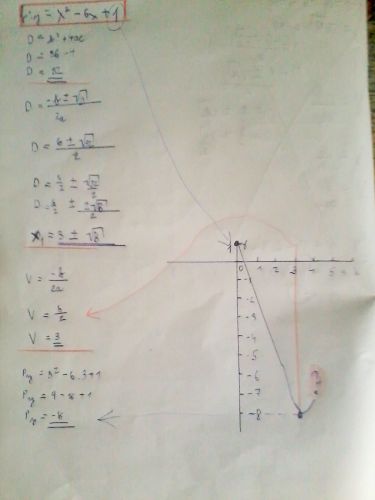
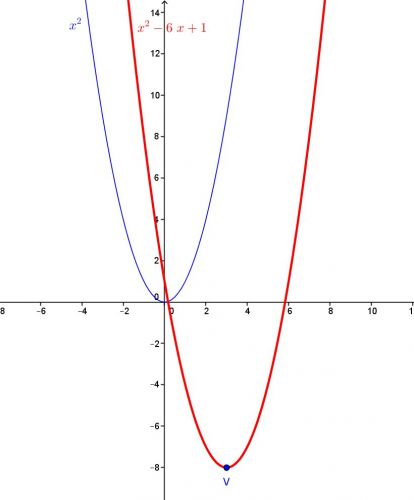
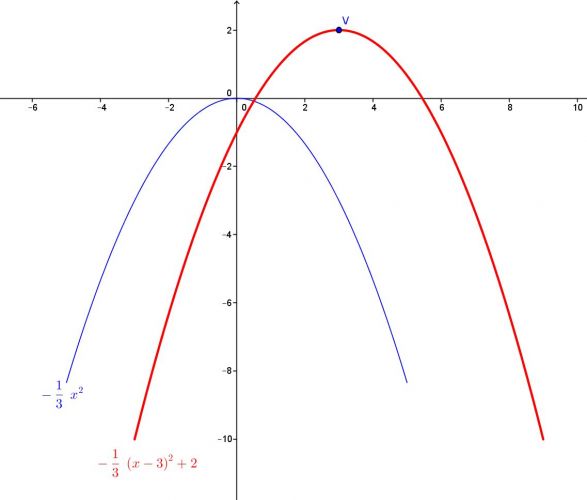
Grafem dané funkce je jedna parabola – ta červená. V prvním odpovědi Kartaginec vysvětluje, že vrchol paraboly se posune z počátku [0; 0] do bodu [ x o ; y o ]. Tak jsem nejprve vykreslil parabolu funkce y = ax 2 (to je ta modrá) a poté ji posunul tak, aby vrchol paraboly byl ve vypočteném bodu [ x o ; y o ].
Vrchol paraboly určíme tak, že vhodně upravíme rovnici kvadratické funkce na tvar y = a(x – x o ) 2 + y o nebo na tvar rovnocenný tvar y – y o = a(x – x o ) 2 , jak uvádí Kartaginec. A z tohoto tvaru pak určíme Vrchol paraboly V = [x o ; y o ].
.
Řešením kvadratické rovnice ax 2 + bx + c = 0 určíme body, v kterých graf funkce protíná osu x .
x 1,2 = – b /( 2a ) ± √ D /( 2a )
Tyto body jsou symetricky umístěné podle osy paraboly. Proto bude mít vrchol x-vou souřadnici rovnu v 1 = –b/(2a).
.
Vy tedy určujete vrchol paraboly výpočtem kořenů kvadratické rovnice . Já je určil úpravou rovnice doplněním na čtverec .
.
Zde je video, jak se hledá vrchol:
Takže druhý příklad mi vyšel 
Zkoušel jsem vypočítat i ten první příklad f:y=x^2 - 6x - 1 Nevím jak vypočítat ten druhý bod na ose X
Už jsem na to přišel.Teď nerozumím tomu 3. příkladu. f:y= -x^2 - 5x +7
Nejde mi tam udělat ten poslední krok. Najít průsečíky osy y. Vychází mi 25,75 a má vyjít 13
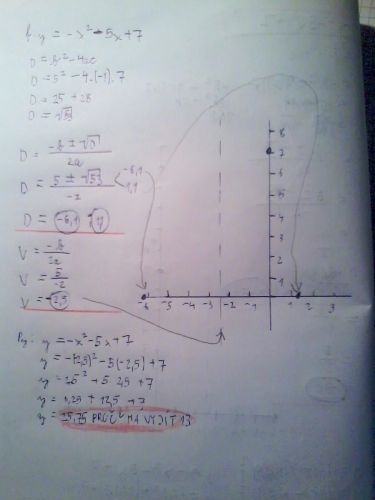
Špatně počítáš.
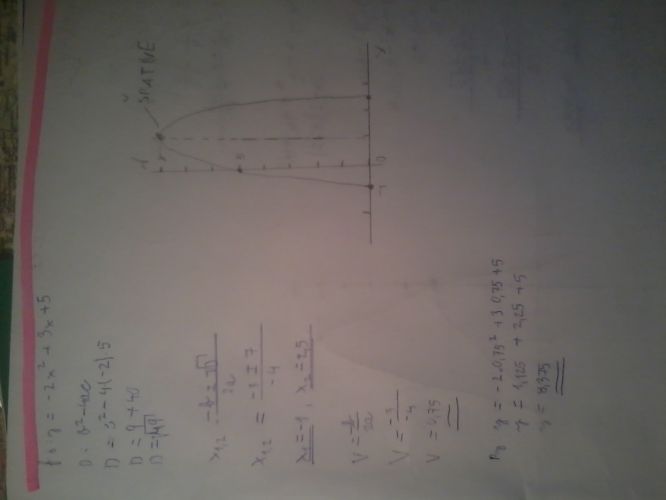
y = –(2,5)2 – 5⋅(–2,5) + 7
y = –6,25 + 12,5 + 7
y = 13,25
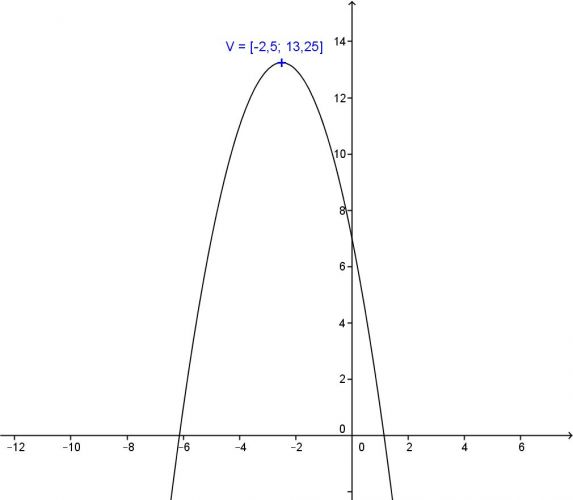
Vrchol bude mít souřadnice V = [–2,5; 13,25] ... tedy o něco více než 13.
doplněno 01.11.14 18:47:Je zapotřebí si uvědomit, že umocňujeme –2,5 na druhou, což dá +6,25. Ale před máme ještě znaménko – a proto – (–2,5)2 = – (+6,25) = – 6,25.
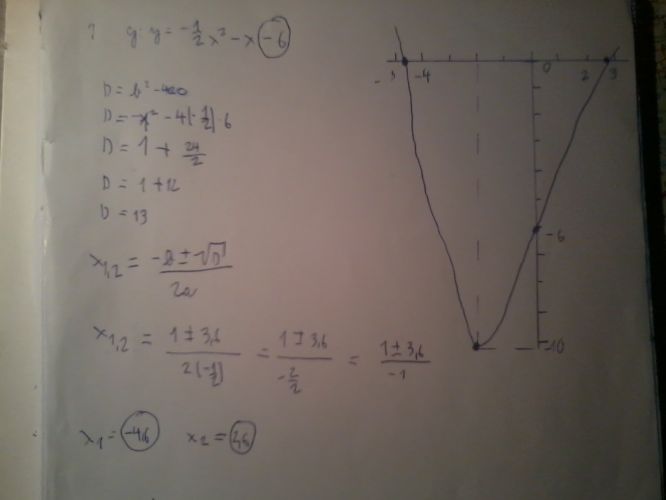
Neporadil by jate mi ještě s tím příkladem se zlomkem -1/3x^2 + 2x -1?
Už jste ho popisoval, ale moc jsem to nepochopil. Mě x1 a x2 vychází -1. . Nějak mi stávkue mobil a nemůžuto vyfotit:-\
Vím, že jsem již otravný. .Emohl by jste se podívat na tyto příklady? Zase mi to nevyšlo.
1)
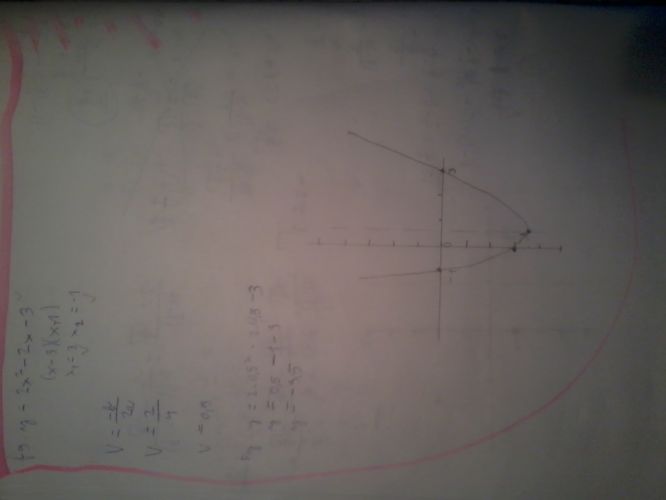
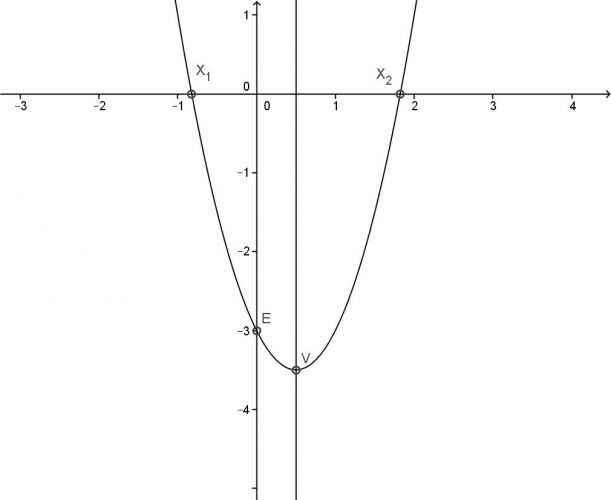
y = 2x2 – 2x – 3
Rozklad je chybný, nevychází celá čísla. Vrchol je určen správně, průsečík s osou y je také správně, ale průsečíky s osou x jsou chybně. Průsečíky vypočti jako u druhého příkladu pomocí diskriminantu.
.
2)
Zde je opět chyba ve výpočtu druhé souřadnice vrcholu:
y = –2⋅0,752 +3⋅0,75 + 5 = –2⋅0,5625 + 2,25 + 5 = –1,125 + 2,25 + 5 = 6,125
Umocňujeme pouze 0,75, poté násobíme –2 a proto vyjde –1,125 a ne +1,125.
Takto lze rozložit výraz x2 – 2x – 3 = (x – 3)(x +1).
Ale my máme výraz 2x2 – 2x – 3 ≠ (x – 3)(x +1).
Abychom mohli provést rozklad podle Vietových vzorců, je nutno upravit rovnici na normovaný tvar: x2 + px + q = 0.
Viz: aristoteles.cz/...
Vrchol je určen správně. Ve vzorci pro výpočet kořenů x1,2 je jen –b ±√D, nikoli –b2 ± √D.
Kořeny vyjdou zaokrouhleně x1 ≐ –0,203, x2 ≐ 0,703
.
Jako žáka střední školy si dovolím upozornit, že je chybné psát by jste – správně je byste.
já bych
ty bys
on by
my bychom
vy byste
oni by
Příště si dám pozor.
Ještě jestli BYSTE mi mohl ukázat jak jste ten zlomek odmocnil. Já umím odmocnit jen celý čísla. Jde ten zlomek odmocnit i bez kalkulačky ( jako poloodmoocnění )?
Dobrý večer,
chtěl jsem se optat zda mám tento příklad správně. Zkontroloval bych si to sám podle geogebry, ale neumím zadat zlomek.
Děkuji
Diskriminant vychází záporně, tudíž funkce neprotíná osu x.
D = (-1)2 – 4⋅(– ½)⋅(–6) =1 – 12 = – 11
x-vá souřadnice vrcholu je –1
xV = 1/(2⋅(– ½)) = – 1
Proto další výpočty jsou již chybně.
1x
Zatím tam žádnou přílohu nevidím, ale obecně: grafem kvadratické funkce je parabola; základní případ je y = ax2, což je parabola s vrcholem v počátku otevřená nahoru pro a kladné, dolů pro a záporné.
Obecný případ pomocí doplnení na čtverec převedu na tvar
y - y0 = a (x – x0)2
což říká, že vrchol se posune do bodu [x0,y0] , což je vlastně počátek soustavy souředné, kterou dostanu substituci
(x – x0) = x’, y - y0 = y´
Rovnici funkce upravíme:
y = x2 – 6x + 1 = x2 – 2.3x + 9 – 8 = (x – 3)2 – 8
Vrchol paraboly bude V = [3; –8]
Mohl bych Vás ještě poprosit o ten 4. příklad? Zbytek si zítra pokusín udělat.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.