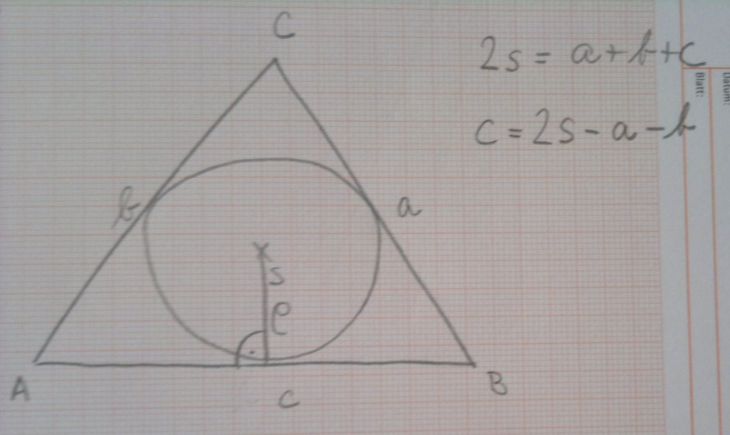
Dobrý den, nevíte prosím, jak toto vypočítat? Děkuji
1x
A co kdybych na takové zadání odpověděla, že tečna je přímka a přímky jsou nekonečně dlouhé?
0x
No iak to opravdu nevím.
Uvažujme: znám pouze obvod trojúhelníka. Pokud jsem schopen vypočítat télku tA tečny z bodu A jako t = f(s) tak prostým přeznačením (třeba A → B, B → C, C → A nezměním s a tedy tečny tB, tC vyjdou stejně dlouhé a tedy rojúhelník je rovnostranný (sic!)
Je zadání úplné?
doplněno 29.10.14 21:20:Možná lze zadání chápat i tak že znám též poloměr kružnice vepsané. Ale anito nemění nic na předchozí úvaze.
doplněno 30.10.14 23:34: No, po úvaze docházím k názoru, že problém příkladu je spíš v zadání než v řešení. Výraz s – a, který vypátral x, je v celku triviální, ale představuji si, že je spíš řešení problému najít nějaký vztah pro tu tečnu (schválně to formuluji takhle nejasné) než odpověď na otázku "vypočtšte délku". V tom nemohu než souhlasit s komentářem x "Jak výsledek chápat, když velikost strany a není známa?" Mimochodem, všimli jste si, že v toto výsledku vůbec nevystupuje ró? A jen pro zajíémavost, ten výsledek lze zapsat i jinak: s – a = ½(b+c–a)doplněno 30.10.14 23:45:
A pokud bych chtěl přeci jen nějak zkoumat závislost na poloměru, zjistil bych toto: Při daném ró dosýhne s minima pro rovnostranný trojúhelník (to lze jednak očekávat, jednak ověřit různými způsby, například aplikací Lagrangeových multiplikátorů na vzorec který uvádí dejavu. nebo i jiný podobný.. Takže pokud je s menší než toto minimum, úloha nemá řešení, je-li mu rovno, je řešení jediné, a pro větší s celkem snadno (úvahami o extrémech) zjistím, že řešení je nejednoznačné a příslušná délka tečny může být libovlná v uršitém rozmezí okolo té dálky, odpovídající rovnostrannému trojúhulníku (které je tím větší, čím větší je s¨. příslušné úvahy neuvádím, ideově jsou jasné, ale technické provedení by přeci jen bylo delší.
Zadání jsem nalezl rovněž zde – Příklad 2–1
Je zde i nápověda a řešením je zde s – a.
Jak výsledek chápat, když velikost strany a není známa?
Podle mne znám ještě poloměr té vepsané kružnice ró. tA pak bude f(s, ró) s tím, že f asi není funkce (tj. jednoznačná) - vychází mi, že poměr s/ró je součtem cotangent polovin všech úhlů hledaného trojúhelníka. Při troše štěstí a moři času na úpravy goniometrických vztahů může taková rovnice dát konečný počet řešení pro ty úhly a z nich pak půjdou vypočíst délky jednotlivých tečných úseček.
Máte rozhodně pravdu v tom, že úloha může a pravděpodobně má být chápána tak, že je zadáno i ró. Nicméně pokud by řešení bylo jednoznačné, stejně by trojúhelník musel být rovnostranný, čili mělo by být víceznačné. Jinak takto ta úloha nemusí být řešitelná vůbec, když byde ro příliš velké, může se stát, že zadané s nebude vyhovovat, a to dává náznak, že ta úloha není zas tak nesmyslná. Zajímavá je též poznámka x, ale na to se podívám, až se vrátím od doktora (on na to x bude určite stačit, aby si to rozebral).
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.