Nejste přihlášen/a.
Dobrý den, mám k Vám prosbu.
Včera jsme ve škole začali dělat Funkce : Absolutní hodnota. V hodině jsem dělali s grafem, který jsme pak různě přemisťovali. Vůbec tomu nerozumím, proč se ten graf nejdříve pohnul doleva a pak dolu.
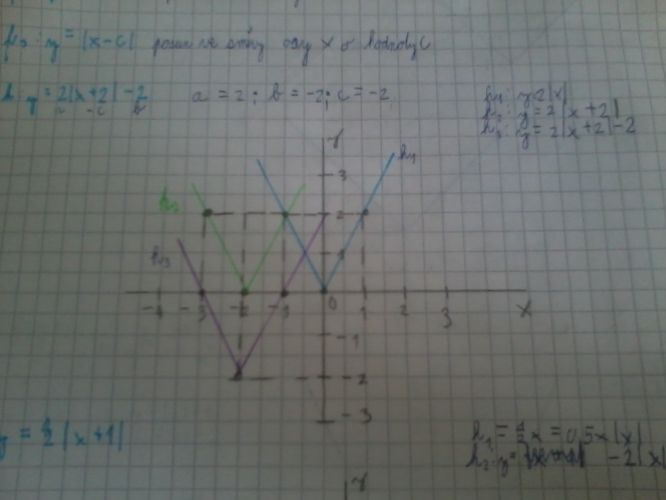
Zadání h:y = 2 |x+2 | -2
dál jsme si tento předpis nějak rozdělili na tři části:
h1:y= 2 |x |
h2:y = 2 |x+2 |
h3:y = |x+2 |-2
Nevím jak to více popsat. Hledal jsem v učebnici, ale tam jsem to nenašel![]()
Děkuj
0x
Asi takhle: Základní pro počítání s absolutní hodnotou je znát samo definici, tedy
|x| = x pro x>0,
|x| = 0 pro x =0
|x| = –x pro x <0
(ten případ x = 0 lze zahrnout pod první řádek, když místo x . 0 napíšeme x ≥ 0, nebo podobně k poslednímu řádku), no a pak graf , který vypadá podobně jako ten tvůj první graf, jen je "méně špičatý", viz přiložený obrázek.) To ostatní, co jste prováděli, není zvláštnost absolutní hodnoty, ale využívá toho, že si rozmyslíme, co uděljí s grafem funkce y = f(x) , když budeme zkoumat funkci f1, která je dána vztahem y–a = c. f(x–b) Zkus zapřemýšlet o tomto (uvažuj substituce souřadnic), já se k tomu ještě vrátím.
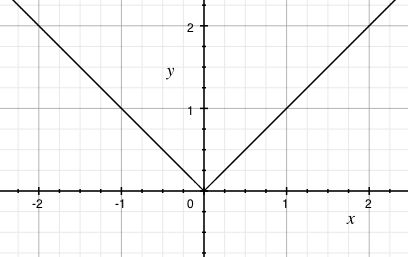
Takže k těm kouzlům. Nejdřív posunutí v iksu, tj. místo y = f(x) vyšetřuji y = f(x – b) , tedy a = 0, c = 1. Označím- li x – b = x’, tak vlastně vyšetřuji původní funkc, ale zakreslenou v nových souřadnicích x’, y. Jaký je jejich vztah k původním? Mají jiný počátek, když x’ = 0, tak x = b, čili nový počátek je ve "starém" bodě [b,0] a o to b se taky posunul graf funkce f doprava. (Když to aplikuji na abs. hodnotu, tak |x| měla špičku v nule, a |x–b| má špičku v x = b, specíálně |x+2| je absolutní hodnota, posunutá o dva doleva (b = –2, špička v bodě x = –2)
To ostatní si snad promyslíte sám. Vy jste vlastněě začínali násoběním dvojkou, y = 2f(x). To je změna měřítka v ose y, ty přímky z grafu abs. hodnoty stoupají rychleji. A posuv y = f(x) – 2 neboli y + 2 = f(x) posune graf o dvě dolů.
Tož tak.
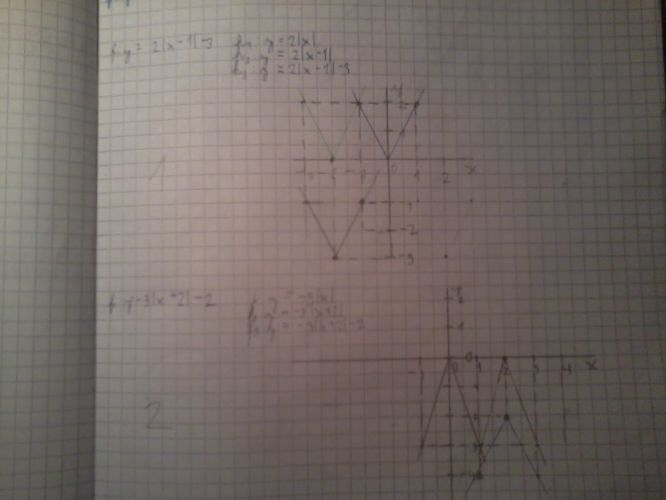
TOMU DRHÉMU PŘÍKLADU ROZUMÍM JE TEDY DOBŘE?
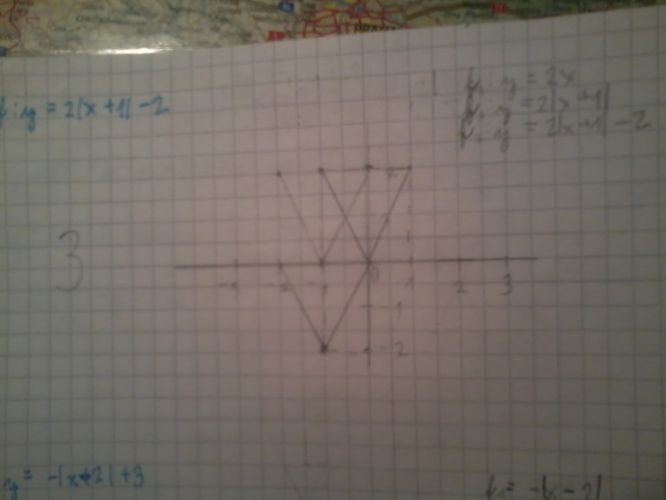
U toho 3. příkladu PROČ SE mi zase ten obsah posunul po ose X o jedno číslo vlevo, když dle zadání |x+1| se měl obsah přesunout o jedno číslo vpravo?
V prvém příkladě vidím zadání y = |x – 1|. Tudíž graf se posune vpravo do +1 na ose x, tak jak správně říká Kartáginec. Ten graf je tedy špatně narýsován.
U 3. příkladu je v zadání |x + 1|, takže se graf posune opačně, než v 1. příkladu, tedy do čísla –1.
Ve škole jsme si říkali, že když je př |x-1| tak se graf posune vlevo. Když je |x+1| tak se posune vpravo.
graf se tady neposune doleva jak jste psal , ale doprava
Jelikož je |x + 2| tak doleva do –2. Dále je 3|x + 2| – 2 a proto se ještě posune o 2 dolú. Vrchol bude mít souřadnice [–2; –2]
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.