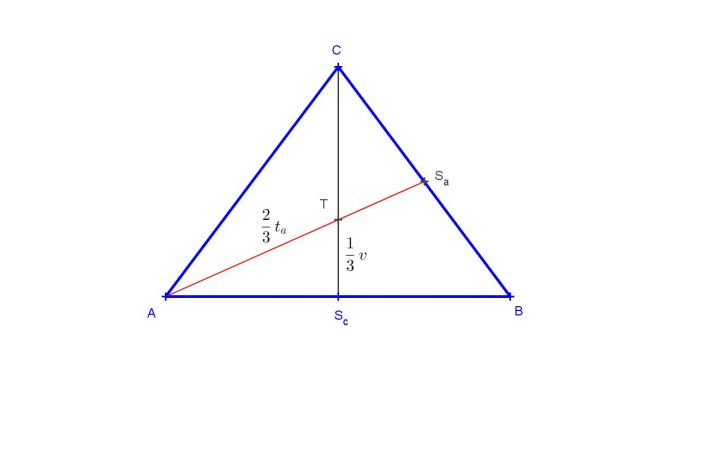
V rovnorameném trojúhelníku se základnou 60 a obsahem 1200 vypočtěte těžnici k ramenu
vypočítala jsem si výšku vc = 40 a pak zbylé dvě strany a,b = 50 ale dál newím jak pomocí toho nějak tu těžnici vypočítat
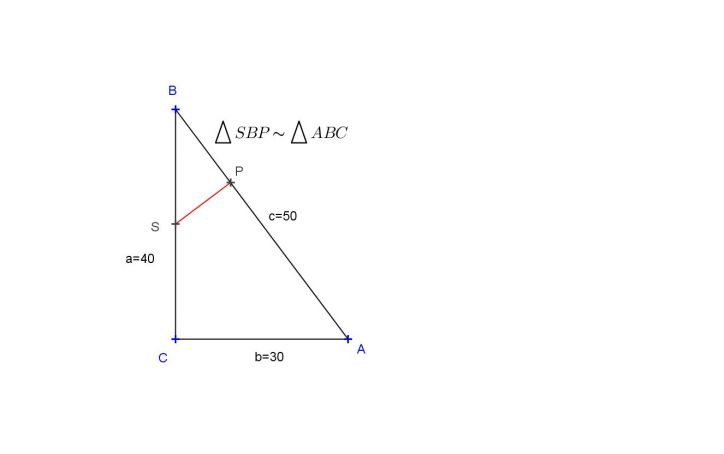
doplněno 13.09.14 20:25:ještě mám problém s pravoůhlým trojúhelníkem s odvěsnami 40 a 30. Jak daleko od přepony se nachází střed delší odvěsny?
ta vudálenost od toho středu k té straně musí být kolmá? Zkusila jsem to přes třední příčky, vznikl mi menší trojúhelník vypočítala jsem přeponu 25 a ais bych měla vypočítat výšku?
Možná doplním, (nejspíš zbytečně, a tazatelce je to i tak jasné, ale pro jistotu), že je to díky tomu, že trojúhelník ABC je rovnostranný a že tedy úsečka ScC je současně těřnice i výška.
Jiná možnost je spočítat obsah trojúhelníka ABSa ze známé základny a výšky a porovnat s Heronovým vzorcem, v někž neznám právě jen těžnici.
1x
Nejlépe bude využít podobnosti ΔSBP ~ ΔABC. Koeficient podobnosti je 20/50 = 2/5. Strana PS bude mít velikost 30 ⋅ 2/5 = 12. A toto je současně vzdálenost středu S od přepony AB.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.