Nevím jak podle zadání nakreslit graf vectoru, vyšlo mi, že (A,B) = (3i2) Nevím jak to nakreslit do grafu, a potom nakreslit 3 orientované úsečky, které jsou umístěním vectoru. Vůbec to nechápu, cos tím dělat. vypočítat to podle vzorečku umím, ale nakreslit to vůbec neumím. Problém je také v tom, že jsme rozdělení na dvě skupiny a většina třídy maturuje z matematiky, a mají 2 matiky navíc, které já nemám, takže to ani učitel moc nevysvětloval. Děkuji za pomoc. 
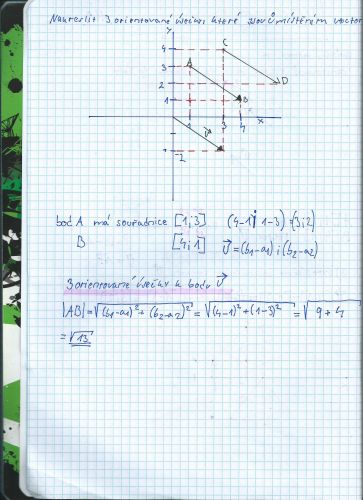
Ke druhému obrázku.
Takhle vypadal další obrázek, ale fakt nevím, kde se ty čísla vzaly apod. Je to jen překreslené.
0x
Ale to vás mají učit ve škole!
Stručně: Vektor (proč to píšeš s "c"?) je "úsečka", která má směr a velikost (délku). V pravoúhlé soustavě souřadnic se dají tyto vlastnosti zapsat pomocí jakoby souřadnic vektoru, vektor (3;-2) například v podstatě znamená "ve směru X o +3 a ve směru Y o -2".
Vektor může být zadán i dvěma body, pak se ale musí říct, ve kterém bodu je začátek. Když bude začátek v A=[7;2] a konec v B=[5;6], tak ten vektor je B-A=(5-7;6-2)=(-2;4). Tzn. když vyrazíš z A a posuneš se o ten vektor (-2;4), tedy o -2 ve směru X a o +4 ve směru Y, dostaneš se do bodu B (fakt to souhlasí, zkus si to).
Vektor pak můžeš namalovat kamkoliv, když začneš (dáš mu počátek) třeba v bodě [0;0] (v počátku souřadnic), bude končit v bodu [-2;4] (asi mu pak říkáte centrovaný vektor, jak se zdá). Když ho umístíš do bodu [-10;-9] bude končit v [-10-2;-9+4]=[-12;-5]; toto asi pak nazvete umístěním vektoru (-2;4) do bodu [-10;-9]. Není to složité.
Pozn.: Vektor se píše do kulatých závorek, oddělovačem čísel není "i" ale středník. Takže ne
u=(b1-a1)i(b2-a2) jako na druhém obrázku, ale
u=(Bx-Ax ; By-Ay).
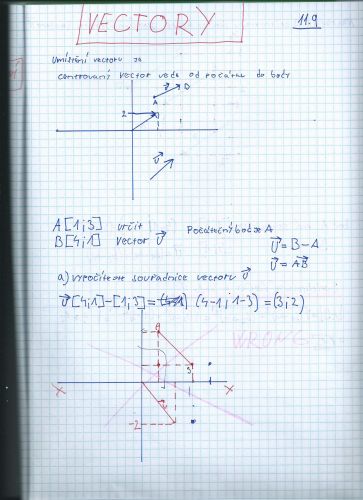
Pozn. 2: V 1. obrázku ten vektor není (3;2), ale (4-1;1-3)=(3;-2) a obrázek máš blbě (koneckonců je to u něj poznamenané). Teď už si ho určitě nakreslíš lépe.
Děkuju moc, ale já to nějak nechápu. Takže teoreticky, bych mohla si nakreslit na tom křížku kdekoliv ten začátek a akorát tam dát ty čísla? A já vůbec nevím, jak ten obrázek 1 nakreslit dobře. A jak poznám kde je bod a1,b1,a2 a b2? To podle těch souřádnic? A takže u toho prvního je blbě i výpočet? A fakt děkuju, jenže matematika jde mimo mě. 
Měla jsem pocit, že vektor je s C, prtože to není český slovo.
Přiklad 1: vektor "u" piš se šipkou nad písmenem
A=[Ax;Ay]=[1;3]
B=[Bx;By]=[4;1]
u=B-A=(4-1;1-3)=(3;-2)
Centrovaný vektor = vektor "u" umístěný do počátku: začíná v bodu [0;0], končí v bodu [0+3;0-2]=[3;-2].
Vektor "u" umístěný třeba do bodu [1;2] začíná v bodu [1;2] a končí v bodu [1+3;2-2]=[4;0].
Vektor "u" umístěný třeba do bodu [-7;3] začíná v bodu [-7;3] a končí v bodu [-7+3;3-2]=[-4;1].
Tím křížkem myslíš souřadné osy, vodorovně osa "x", svisle osa "y", protínající se v bodu [0;0]?
Jestli kdekoliv začátek? Asi ano, když není uvedeno, kam máte umístit ten vektor "u", ale jen, že ho někam máte umístit, tak si zvol, kam to bude. Kdyby řekli "umístěte počátek vektoru (umístěte vektor) do bodu [...;...]", tak bys ho musela umístit přesně podle zadání.
Body je lepší si psát [Ax;Ay], než nějaké [a1;a2]. Z toho prvního zápisu je hned jasné, která souřadnice se odměřuje na které ose (ta první bývá na ose "x", druhá na ose "y", v prostoru by pak třetí byla na ose "z" (ale to ještě nemáte)). Jo, ta čísla Ax apod. jsou souřadnice.
Snad ti nepletu vaši terminologii.
Díky, snad to už trochu chápu, ono by to nemělo být těžké. Údajně jsme až o rok pozadu a u některých škol i o rok a půl. A také to berem jen obecně, jenže učitel to neumí vysvětlovat. A moc děkuju, musíš bejt génius. ) A jo tím křížkem myslím to, jen jsem nevěděla jak to zformulovat, vím že to je gaussova něco, jenže to se mi moc nelíbí.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.