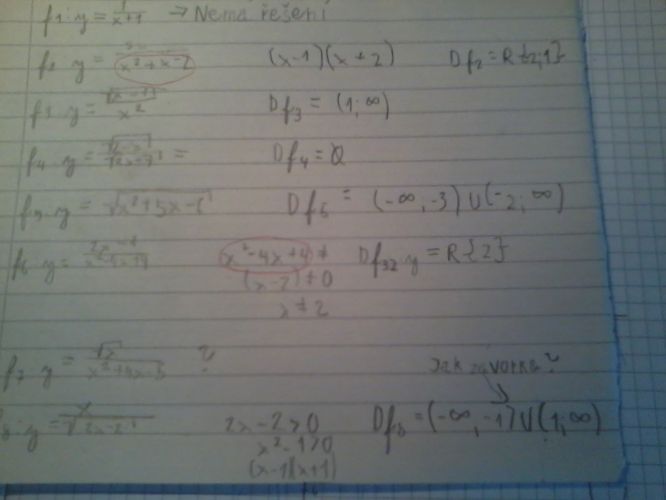U těch úloh nerozumím jak k tomu dojdu.
V úloze f2,5,7 si nemůžu vzpomenout jak byl.
Děkuji.
3x
Nevím, jestli rozumím dotazu. Hledá se definičné obor funkce, tzn. "x", pro která má funkce smysl? Jestli ano, tak:
2) Jmenovatel zlomku nesmí být 0 (nulou nelze dělit). Výraz ve jmenovateli se dá zapsat jako součin těch dvou uvedených závorek, takže nulový vyjde pro x=1 a x=-2. Definiční obor funkce jsou tedy reálná čísla bez 1 a -2.
5) Výraz v odmocnině nemůže být záporný (pracujem-li v oboru R). Podle naznačeného řešení to vypadá, že zadání má být: odm(x^2 + 5x + 6). Tento výraz pak má dva nulové body x=-3 a x=-2 a mezi nimi je záporný. Definičním oborem by pak byly intervaly "-nekon. až -3" a "-2 až nekon.", -2 a -3 tam také patří, ne jak je na papíře. Kdyby v odmocnině bylo opravdu -6, jak je na papíře, bylo by vše jinak.
7) Podle čitatele musí být x nezáporné (0 a větší), jmenovatel je nečitelný, ale zas: nesmí být nulový.
Jen se ještě zeptám na toto. V příkladu f6 je číslo x^2 - 4x =4
Jak z toho vzniklo toto? (x-2) =0 . Podobný to je ještě u dalšího příkladu f2 a f5.
6) není x^2 - 4x =4, ale máme výraz "x^2 - 4x +4". A ten se dá napsat zas jako součin závorek, tentokrát (x-2)*(x-2), takže nulový bod toho výrazu je vlastně jen jeden: x=2.
A 2) už jsem přece popsal.
Já se ještě ptAm jak udelat ten součinový tvar nemůžu si vzpomenout.
Př x^2 - 4x +4 jak z toho udělám to (x - 2)^2?
Nebo x^2 + 4x -5 jak z toho udělám to (x +5) ( x -1)?
No, probírali jste úpravy výrazů a jejich přepisy podle vzorů (a+b)^2, a^2 - b^2 apod., takže byste to měli mít trochu "v oku" a odhadnout to, nebo aspoň rychle prubnout, který se zrovna hodí.
V praxi jsou ovšem tyto vzory málokdy použitelné, takže se používá obecný vzorec pro výpočet kadratické rovnice. A když už máš výsledky, tak nemá cenu je zapisovat jako součin nějakých závorek (to už by byla jen práce navíc). Ale škola je škola a procvičit se ve výrazech a závorkách je potřeba.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.