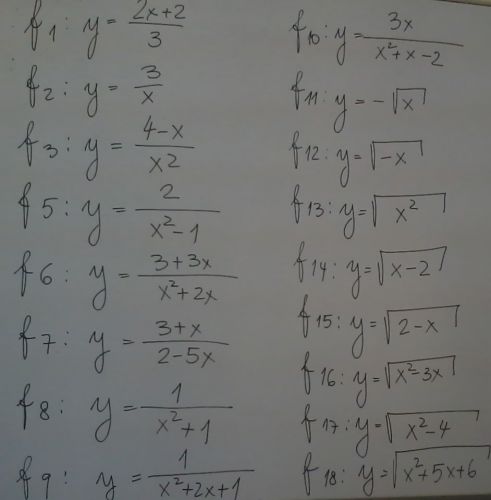Dobrý den,
doma jsem našel tyto příklady, ale vůbec nevím jak je zapsat![]()
Mohly by jste mi prosím poradit? V Obrázku je zadání. Mělo by to být snad dost vidět.
Nemusíte mi říkat všechny příklady to né, ale jen poradit
Moc Vám děkuji
Chytil jsem se jen u nějakých![]()
Df1=R
Df3=R - ( 0 )
Df5 = 1
Df11 = (0- nekonečno)
Df13 = R
0x
Df3 je myšleno dobře, ale ta nula se píše do vlnitých závorek, jako množina, obsahující bod 0 a nic jiného. Také lze D zapsat jako sjednocení intervalů: Df3 = (–infty, 0)U (0, infty) (zde infty značí nekonečno a U, samozřejmě, je znak sjednocení). Stejné je Df2. Df5 je úplně blbě. Zde se x nesmí rovnat ±1, takže Df5 = R – {–1;1} Nebo jako sjednocení intervalů). Df11 je tvořen nezápornými x, což lse zapsat třeba jako < 0, +infty), případně jako {x€R|x≥0}; vašemu zápisu nerozumím. Df12 je podobné, jen s nekladnými x, čili (– infty, 0>. Df13 máte dobře.
Děkuji. Příště si dám pozor na závorky.
Mohly by jste mi ukázat jak na další příklady.
Nějak se v tom ztrácím.
A v čem je problém? zjistit podmínky, kdy je funkce definovaná (zde hlavně vyloučit dělení nulou), případně zjistit, kdy je výraz pod odmocninou kladný), anebo ty podmínky zapsat?
Takže byto osi chtělo promyslet si způsoby zápisu množin. Zkusím něco shrnout.
Jak víme, množina je soubor nějakých objektů, a je určena svými prvky (tohle není ani tak definice (definuje množinu tak, že toto slovo nahrazuje slovem soubor), jako takový názorný popis k podpoře naší představivosti; nemůžeme ostatně definovat všechno, z něčeho musíme vycházet, třeba Euklides pokládal za základní pojmy bod, přímku, rovinu...
Takže, některé způsoby zápisu množiny:
a). výčtem, Použitelné u například konečné množiny. Prvky množiny zapíčeme do vlnitých závorek, oddělené středníkem. Třeba přirozená čísla od jedné do šesti včetně zapíšeme {1;2;3;4;5;6}. (S jistou volností tak můžeme zaúsat i spočetné množiny, třeba přirozená čísla jako {1;2;3;4;...}, ale o tom se raději nebudu bavit, je to trochu složitější. A množina, která neobsehuje žádný prvek, se označuje Ø a jmenuje se, jak každý ví, množina prázdná.
b) vlastností: {xεM; V(x)}, případně {xεM| V(x)} označije množinu prvků z nějaké univerzální množin M, které mají vlastnost V(x) (zde jsem použil epsilon jako znak "patří do množiny"), například kladná reálná čísla lze napsat jako {xεR;x>0}
Zatím tak, promyslete si intervaly. Doplním později.
Tak teď k těm intervalům. To asi v podstatě znáte, takže shrnu: mám li dvě čísla a < b, reálná nebo symboly plus či mínis nekonečno, tak všechna reálná čísla mezi a, b (včetně či nevčetně) se jmenují "interval". Jestliže číslo a do intervalu patří, tak u něho uděláme špičatou závorku < pokud tam nepatří, kulatou (. (existuje i druhá možnost, kterou někteří autoři preferují z typografických důvodů, psát místo < hranatou závorku [, místo kulaté závorky psát ]. U čísla b, které patří do intervalu , děláme špičatou závorku> nebo hranatou ]. když tam nepatří, tak ) nebo [ , Bez intervalů bychom se vlastně mohli obejít, například platí < 2;6) = {xεR; 2 ≤ x < 6}, ale zápis pomocí intervalů ja pro reálná čísla přirozenější a preferovaný.
Pomohlo vám to? Když tak položte konkrétní dotaz, nechce se mi rozepisovat všechny vaše definiční obory. Snad mych jen řekl, že definiční obory lze zapsat různě, ale snažíme se o zápis pomocí sjednocení disjunktních intervalé, případně s odečtením vyloučených bodů.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.