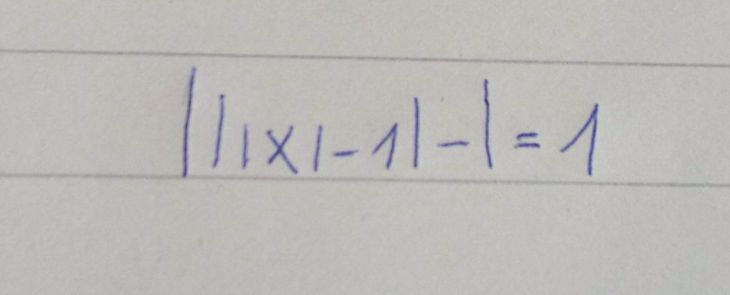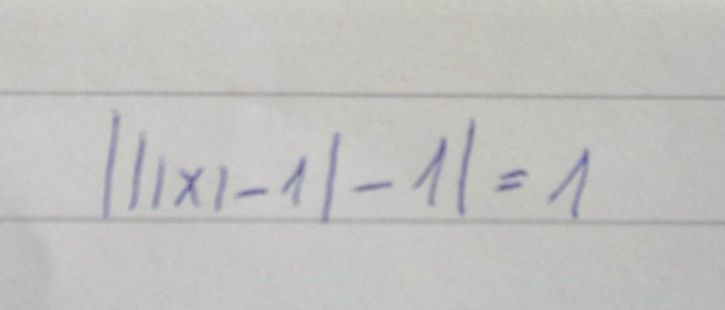Dobrý den, jak se prosím vypočítá tento příklad? Děkuji
doplněno 05.09.14 09:27:Omlouvám se, ten 1. obrázek se špatně
3x
Musíš si to vždycky rozložit na oba případy. Tedy v prvním kroku (odstraneni prvni absolutni hodnoty) se ti to rozpadne na 2 případy:
1) | |x| - 1 | -1 = 1
2) | |x| -1| -1 = -1
Upravis si prvni pripad a vyjde ti: | |x| -1 | = 2 a zase to rozlozis na oba pripady:
1.1 : |x| -1 = 2
1.2: |x| -1 = -2
Z 1.1 ti vyjde |x| = 3 a zase to rozlozis na 2 pripady:
1.1.1 : x = 3
1.1.2 : x = -3
a to už je řešení té první větve. Takhle postupně spočítáš všechny větve.
doplněno 05.09.14 10:31:Když ti např. z 1.2 vyjde: |x| = -1, tak to zjevně nemá řešení, protože absolutní hodnota nemůže být záporná.
2x
Musíte odstranit abs. hodnoty, což se dělá tak, že rozdělíte reálnou osu nna množiny, v nichž výraz uvnitř abs. hodnoty nemění znaménko, a v těchčástech, kde je výraz uvnitř abs. hodnoty kladný /nezáporný), abs. hodnotu vypustíme, a tamk, kde je záporný, změníme u nej znaménko (vynásobíme –1) a pak abs. hodnotu vypostíme.
Pokud je v příkladu jen jedna abs. hodnota, je to jednoduché, je-li jich více, pak po odstranění jedné pracujeme na dalších. U vás třeba začneme výrazem |x|: pro x>0 je |x| = x a řešíme rovnici ||x–1| – 1| = 1 (začneme rozborem kladnosti výrazu x –1, ovšem v oboru kladných (nezáporných) čísel), atd.
Jak jsem koukal, mezitím odpověděl ignify, jen na rozdíl ode mne začal od vější abs. hodnoty.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.