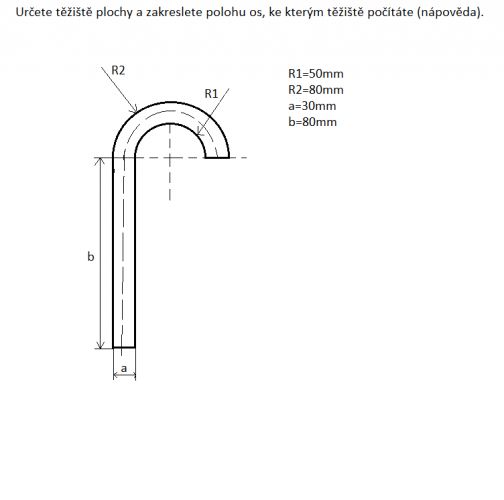
Ahoj, pomohl by mi prosím někdo s tíhmle? Nevím jak zvolit ten počátek těžiště..To je ten průsečík os? A dále když je jedna plocha pod osou, tak se to odečte?
3x
Jaký počátek těžiště? Na to se vás nikdo neptá. Víte, jak se těžiště počítá? Máte k disposicy dvojný integrál? Pak počítáte těžiště jako bod, takový, že plocha soustředěná do tohoto bodu má k osám souřadnm stejný moment (což je součin plochy S se vzdáleností těžiště od těch osú jako integrál z elementárních momentů vzhledem k těmto osám /tedy xt*S = intpřes plochu x dS (moment k ose x), analogicky k ose y. Ty osy si můžete zvolit jak chcete, vyjde to vždy, takže si je zvolíte tak, aby se vám to počítalo co nejlépe. Možná tak, ře střed souřadné soustavy položíte do středu těch dvou polokružnic a osy zvolíte: osa x vodorovně, osa y svisle, aLE JDE TO I JINAK, TAKY BYSTE MOHL POČÍTAT EXTRA TĚŽIŠTĚ TOHO "OHNUTÉHO DRŽADLA" A EXTRA TĚŽIŠTĚ TÉ "ROVNÉ HOLE" A PAK VYPOÍTAD TĚŽIŠTĚ TĚCH DVOU "PARCIÁLNÍCH TĚŽOŠŤ"
(Omlouvám se za capslock, ale už se mi to nechce přepisovad, snad to přežijete.)
Je tedy správně toto?:
S1=a.b= 2400mm2
S2= pí.R2 na druhou=20106mm2
S3=pí.R1 na druhou=7853
xt1=-65mm
xt2,xt3=0mm
yt1=-40mm
yt2= 4R2/3pí=33,96mm
yt3=21,2
xT= 2400/14653 = -10,65mm
yT=753283,36/14653=51,4mm
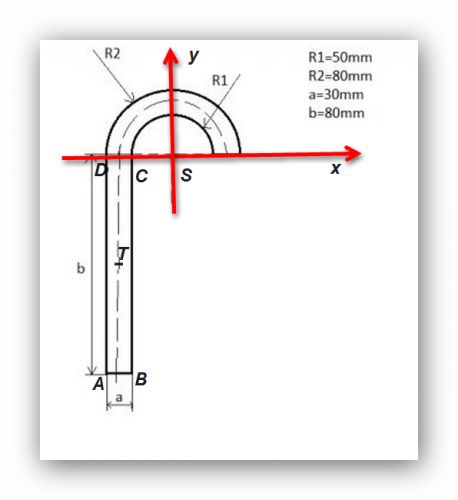
Tak mám.li posuzovat, jestli je to správně, musím především vědět, co je co. Předpokládám, že jste zvolil osžy souřadné tak, jak jsem radil (viz obrázek), S1 že je obsah obdélníku ABCD, S2, S3 postupně obsahy kruhů o středu S a poloměrech R2,R1 (tady ovšem cítím nebezpeči. v úloze pracujeme s polokruhy) T1 =[xT1, yT1] těžiště obdélníku ABCD a T2, T3 a odpovídající iksy a ypsilony by měly snad být těžště těch (kruhů? půlkruhůé, T celkové těžiště.
Tolik k označení. Co se týče správnosti, to se musím podíved podrobněji, Vy tam nemáe žádný postup, a podezřelé je mi, že tam nevidím žádný integrál. Může tam být skryt už jeho výsledek, ale jak říkám to ještě posoudím zvlášť.
my jsme na takové úlohy vůbec nepoužívali integrály, a postup tam je, jenom jsem to moc nerozepisoval ,ale snad je to z toho jasné..výsledky nemám, kdybych je měl, tak to sem nepíšu
spočítal jsem plochy S1,-obdélník, S2 velký půlkruh, S3malý půlkruh -a ten jsem na konci odečetl
ke všemu jsem vypočetl x a y těžiště..
ale nevím, zda je to dobře ..kdybys se podíval na to prosím
Tak jě se hned ze začátku ptal, jestli máte k disposici dvojný integrál. Z vašwho zápisu se mi zdá, že máte vzorec pro těžiště půlkruhu, tedy víte, že jeho výška nad průměrem toho kruhu o poloměru R je 4Rπ/3 . Tento vzorec tam zřejmě používáte, a tento vzorec se právě vypočítá integrací. Vy tedy integrovat neumíte, takže jste si patrně tento vzorec neodvozovali, ale jen řekli, je to tak? (Aspoň já bych ho bez integrálu odvodit nedovedl.) No a to jsem měl na mysli, když jsem říkal, že ve vašem výpočtu není integrál, ale že je v něm skryt výsledek toho integrování, totiž právě ten vzorec. (Možná jsem vás tím spletl, takže jste si myslel, že po vás chci výsledek příkladu, ale to bylo jen nedorozumění.)
Takže shrnuto: souhlasím s tím, jak jste vypočítal těžiště obdélníka ABCD, správně jsou i těžiště půlkruhů o středu S a poloměrech R2, respektive R. Obsahy těch půlkruhů máte špatně, yp, co jste spočítal, jsou obsahu celách kruhů; nicméně souhlesím s tím, že ty výsledky (po opravě, tedy po vydělení dvěma) musíte odečíst, abyste dostal obsah toho "půlmezikruží. A co se týče výsledku pro xt, yt, zde nerozumím, jak jste je získal, zde postup nevidím, a rozhodně to nemůže být dobře, když vám těžiště celého systému (je to ono?) vychází výš než všechna tři dílčí těžiště. A na závěr tam máte nějakou opravu, u které nechápu, čeho je to oprava. Pokud yT, tak nevím, kde jste ji vzal. Takže tady bych prosil podrobnější popis postupu, abych to mohl zhodnotit.
doplněno 01.06.14 20:21:Pardon, 4rR/π3
doplněno 01.06.14 20:22:Ještě blbě, 4R/3π
2x
Já bych shrnul, čeho jsme dosáhli, a pokusil se načrtnout další postup.
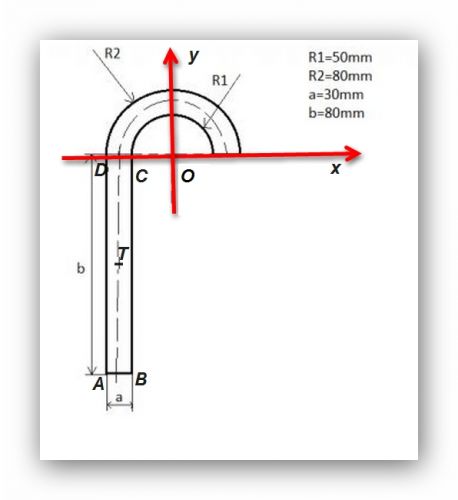
K označení: vycházím z toho, že souřadné osy jsou jako na obrázku výše, jen počátek jsem označil S jako střed kružnic, a to by se mohlo plést s označením obsahů, takže jsem ho přejmenoval na O (viz nový obrázek).
Teď přehled toho, co víme:
Tak předěvším jste spočítal nekteré obsahy:
S1 = ab ... obsah obdélníku ABCD, číselně S1 = 2400mm2
S2 = ½πR2² ,,, obsah velkého půlkruhu . číselně 10053mm2 (tam máte chybu)
S3 = ½πR1² ,,, obsah velkého půlkruhu . číselně 3927 mm2 (zaokrouhleno, samozřejmě)
a doplím
S4 = S2 - S3 = ½π(R2² - R1²) ... obsah "půlmezikruží", číselně 6126 mm2 (omlouvám se, že používám divis místo minus, ale editor poradny to neumožňuje, mínus automaticky předělá da divis).
S = S1 + S4 ... celkový obsah obrazce , číselně 8526 mm2.
=========
Dále jsme zjistili něco o těžištích, napíšu, co vímme a označím, co potřebujeme:
T1 = [xT1, yT1]... těžiště obdélníka ABCD, číselně xT1 = -65 mm , yT1 = -40mm (to je, díky symetrii, prostě střed toho obtélníka
T2 = [xT2,yT2] ... těžiště většího půlkruhu; xT2 = 0 (plyne ze symetrie), yT2 = 4R2/3π (vzorec), číselně 33,96mm
T3 = [xT3,yT3] ... těžiště menšího půlkruhu; xT3 = 0 (plyne ze symetrie), yT3 = 4R3/3π (vzorec), číselně 21,2mm
a potřebujeme
T = [xT,yT] ... těžiště celého obrazce. (Číselné údaje máte, ale zatím je neopisiji, chceme je ověřit).
No a k tomu se nám může hodit
T4 = [xT4,yT4] ,,, těžiště polovičního mezikruží. K tomu zatím žádné číselné údaje nemáme.
Nyní, s vaším dovolením, text uložím (že aby se mi náhodou neztratil) a ve výpočtech budu pokračovat v další odpovědi.
doplněno 02.06.14 17:41:K výpočtu:
Co je to vlastně těžiště? V měchanice definujeme: TĚŽIŠTĚ TUHÉHO TĚLESA JE PŮSOBIŠTĚ TÍHOVÉ SÍLY, KTERÁ PŮSOBÍ NA TĚLESO V HOMOGENNÍM TÍHOVÉM POLI. To znamená, že záleží mj. na hustotě tělesa, a počítá se tak, že u systému hmotných bodů najdeme součet mometnů těchto bodů vůči dvěma osám (například souřadným osám) a výsledek vydělíme součtem hmot; výsledek je vzdálenost od os taková, že moment těžiště je roven součtu momentů hmotných bodů. U tělesa místo součtu pracujeme s integrálem.
V geometrii konstruujeme těžiště (geometrické těžiště, geometrický střed) tak, aby tento pojem odpovídal mechanickému těžišti tělesa, tvořeného daným obrazcem (něco jako plechové mezikruží, například), jehož hustota je konstantní, takže místo hmotnosti pracujeme s obsahem (s objemem ve třech dimensích). Nachácí se v průsečíku těžnic, které půlí obrazec na dvě rovnoploché části. Proto například u obdélníku bude těžiště průsečíkem úhlopříček, nebo středních příček; u trojúhelníku bereme jako základní těžnice spojnice vrcholů se tředem protilehlé strany a podobně. U půlkuhu jedna těžnice bude kolmice k průměru, nad nímž je půlkruh sestrojen, vedená středem (toho jsme v našem případě využili při výpočtu y-nových souřadnic, ale sestrojit jiné těžnice bude asi komplikovanější. Při znalosti počtu infinitesimálního (derivace a integrály) to řešíme právě pomocí dvojného integrálu , ale ten vy k disposici nemáte, a tak jste si, předpokládám, bez důkazu řekli vzorec pro vzdálenost těžíště. (Nebo se mýlím? Poučte mne, prosím.) No a u "polomezikruží je to ještě komplikovanější. Vlastnímu výpočtu, nicméně, věnuji samostatný příspěvek.
Výpočet T = [xT,yT] ... těžiště celého obrazce:
Nejprve vypočtu T4 = [xT4,yT4] ... těžiště polovičního mezikruží. Platí
Pro T2 = [xT2,yT2] platí:
S2*xT2 = S3*xT3 + S4*xT4 ⇒ yT4 = 0 (což je ostatně vidět ze symetrie podle osy x)
S2*yT2 = S3*yT3 +S4*yT4 , odkud
yT4 = (S2*yT2 - S3*yT3)/ S4 , číselně (10053*33,96 - 3927*21,2):6126
No a pro T = [xT,yT] využiji analogický vztah
S*xT = S1*xT1 +S4*xT4 , S*yT = S1*yT1 +S4*yT4 .
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.