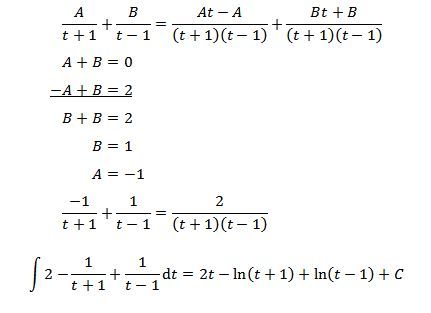Integrál rozklad

A odkud myslíte, že se vzal ten vzorec? Proboha, proč bych to nemohl řešit metodou neurčitých koeficientů? A navíc toto je metoda rozkladu na parciální zlomky, metoda neurčitých koeficientů je až druhotná záležitost, použitá k výpočtu těch parciálních zlomků. A když už o tom mluvíme, 1/(t^2-1) není žádný vzorec, to je racionální funkce, vzorec by z toho byl, až když napížete, čemu se rovná integrál z tohoto výrazu. A pak je to další vzorec navíc, který bych si měl pamatovat.

Doplním, že jsou i jiné cesty, jak integrál poočítat, Například (soustředím se na výraz 1/(t²-1), v němž je jádro pudla):

1/(t²-1) = (t+1-t)/(t²-1) = 1/(t-1) - t/(t²-1)

první člen integruji podle vzorce pro integrál z 1/(t-1) , druhý substitucí t²-1 = y

A kdo jste vy, abyste mi tuhle cestu zakazoval pod záminkou, že se to tak nepočítá?

Prosím, příště važte slova.