Dobrý den,
poslední příklad, který bych potřeboval pomoci vypočítat. Nevím si rady jak na to přijít.
Předem děkuji
doplněno 12.05.14 13:05:I když souřadnice u z by se měla rovnat výšce půlválce a ten poloměr asi bude souviset se souřadnicemi x a y
2x
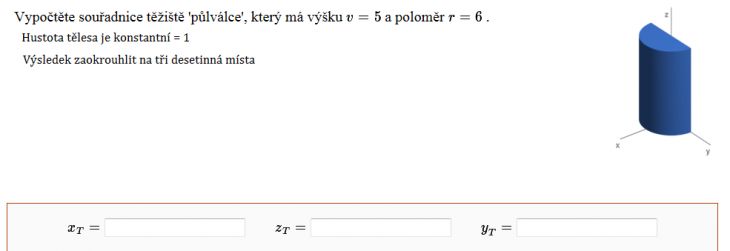
Tohle je sice úloha jakoby třídimensionální, ale vzhledem k tomu, že průřez tělěsa nezávisí na výšce, je zřejmně těžiště v polovině výšky, jeho z-tová souřadnice je tedy zT = ½v. Tím jsme úlohu převedli na rovinnou úlohu, určit těžiště homogenní půlkruhové desky (viz přiložený obrázek).
Těžiště homogenního rovinného útvaru má tu vlastnost, (to je vlastně definice těžiště) , že moment hmoty, soustředěné do těžiště, k libobovolné ose je roven součtu momentů jeho bodů . Kdyby šlo o těžiště systému bodů o hmotnostech mi, tak by pro x-ovou souřadnici těžiště platilo
xTS(mi) = S(ximi)
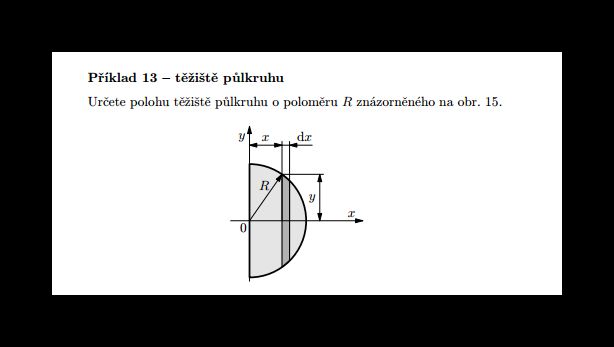
podobně pro y-novou souřadnici (S jako suma. Raději bych napsal velké sigma, ale editor mi ho nenabízí). U homogenního rovinného útvaru sumu nahradíme integrálem, hmotnost obsahem, y-nová souřadnice zde bude, díky symetrii, nulová a vzoreček pro x-ovou souřadnisi vyjádříme nejlépe v polárních souřednicích, viz druhý přiložený obrázek). Potřebný integrál lehce spočteme.
(Více viz třeba v fyzikalniolympiada.cz/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.