Nejste přihlášen/a.
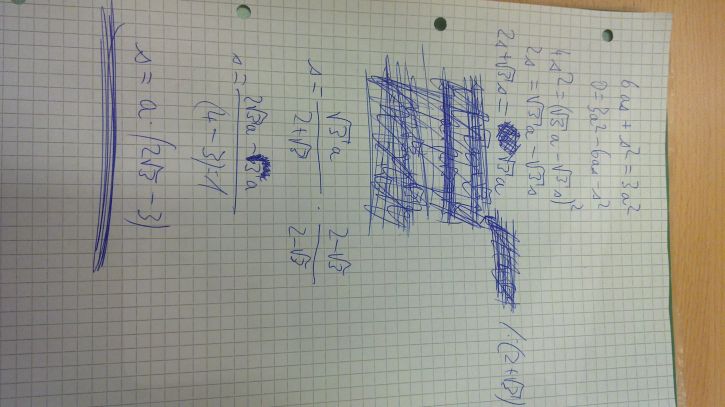
Zdravím, dostali jsme za úkol vyjádřit stranu čtverce vepsaného do rovnostranného trojúhelníka. Počítám, počítám a dopracoval jsem se k rovnici 6as+s2=3a2 a nevím jak z ní to s dostat. Výsledek má být s=a*(2/3-3) a pomocí wolframalpha.com mám ověřeno, že jsem na správné cestě. Díky za každou pomoc.
0x
To vypada jako kvadraticka rovnice pro promennou "s": (s2+6as-3a2=0), tak ji vyres. Me se to nechce pocitat ![]()
Jestli to "s" je delka strany toho ctverce tak to reseni -3 - 2sqrt(3) vypadne, protoze je to zaporne cislo.
Zbyva tedy jen s = a sqrt(3) [-sqrt(3) + 2]
Jak z toho ale dostat ty tvoje "tretiny", to me nenapada ![]()
Jeste znova koukam na ten tvuj zapis spravneho vysledku a napada me, ze to asi nemaji byt "2/3" ale "2sqrt(3)" a pak to vychazi stejne jako pisu o 2 prispevky vyse, jen ja to mam jako "-3 + 2sqrt(3)" a ty to mas zapsane "2sqrt(3) - 3". ![]()
![]()
Ano to s lomitkama je improvizovany znak odmocniny. Dekuju vsem za zopakovanik vysledku, ktery jsem sem uz napsal, ale potreboval bych spis postup.
Ale ten postup snad ignify kompletně napsal, ne? Pravda, nenapsal odvození těch rovnic, ale mám neodbytný pocit, že na to dotaz nesměřoval. Takže pokud potřebujete ještě něco jiného. Napadá mne jedině, že potřebujete postup řešení kvadratické rovnice; nuže, můžete poučít vzoreček x1,2 = (-b ± sqrt (b2-4ac))/2a , což v našem případě dává
s1,2=1/2[-6a±sqrt(36a2+12a2)] = -3a±2a sqrt(3)
jak uvedeno výše. Pravda, možná je příspěvek z 07:55 mailnko matoucí ty rovnosti by měl být chápány spíče s programátorském smyslu, asi takto:
a:=1; b:=6a; c:=-3a2
(prostě ta písmena a v pravých stranách jsou jiná, než vlevo; taky to lze napsat tak, že kvadratickou rovnici s jedničkou u druho mocniny napíšu ve tvaru
x² +px +q = 0
a pak položím p=6a; q=-3a2 )
doplněno 07.05.14 10:59:Tažeta vaše poznámka "Tak jsem si opet zase poradil sam." mi přijde lehce neuctivá, (nebo možná sebeshazující, navozující dojem, že neumíte číst).
S temi prirazenimi a= ... ; b= ...; c=... to opravdu nemam matematicky spravne (neznama "a" tam vystupuje ve 2 ruznych pouzitich), ale ja to psal jen jako takove doplnujici vyjadreni "pro kazdy pripad". Me ani nenapadlo, ze nekdo by neumel dosadit do znameho vzorce pro reseni kvadraticke rovnice ![]()
Tak jsem si opet zase poradil sam.
doplněno 07.05.14 11:52:@kartaginec, Proč sebeshazující? Já se tu nikde postup nedočetl. Určitě ne takový, že bych podle něj postupoval.
Mas napsano, ze jde o kvadratickou rovnici. Jeji reseni urcite znas, jak se pocita a presny postup (po dosazeni do zakladniho vzorce) je i ostatne popsan v mem prispevku v 8:00. Kartaginec ti to navic jeste rozepsal i s uvedenim obecneho vzorce ( [-b ± sqrt(b^2 - 4ac)]/2a ). Ted uz je to rozepsane do podoby, v ktere se to deti uci ve skole, kdyz poprve slysi o vzorci pro reseni kvadratickych rovnic. Podrobneji uz to zapsat nejde. ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.