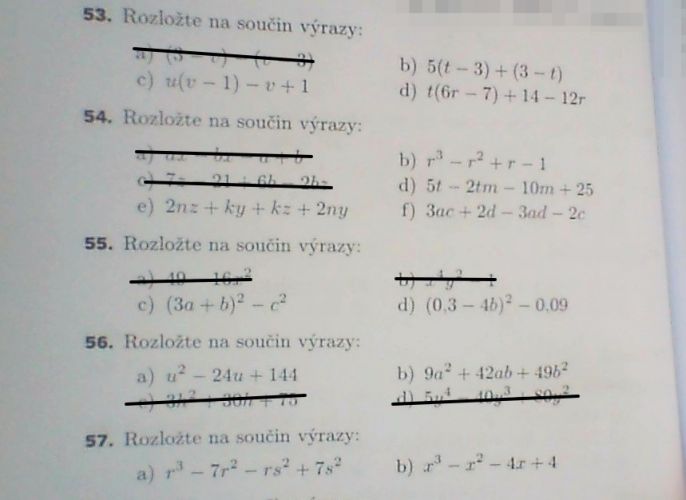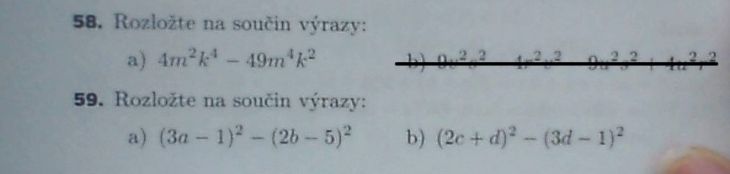Nejste přihlášen/a.
Dobrý den. Už tu píšu po xté kvůli mnohočlenům, protože ve spoustě věcí nemám furt jasno. Doufám, že vás tím neotravuji. Potřebovala bych vysvětlit na jakém principu mám rozložit na součin tyto příklady (foto dole) přeškrtané příklady jsem zvládla, ale nevím jak na zbytek. Potřebovala bych u každého typu úlohy vysvětlit jak na to a zbytek snad už zvládnu. Budu moc vděčná za každou pomoc ![]() děkuji.
děkuji.
0x
Uloha53: vytkni -1 z druhe poloviny vyrazu
54b: vytkni r2 z prvnich 2 vyrazu.
54c: Snaz se vzdycky spojit vyrazy, ktere maji neco spolecneho. Treba v pripadu "a" jsou to 2ny a 2nz, ktere maji spolecne to "2n". Vytkni to. Ze zbytku vytkni "k".54d: z "-2tm - 10m" vytkni "-2m"
54f: stejna rada jako 54c
55:rozloz podle vzorce x2-y2=(x+y)(x-y); (x=3a+b; y=c)
56: pouzij vzorce a2±b2
57a: z prnich 2 vytkni r2, z druhych 2 " -s2 "
57b:opet vytkni x2 a -4
58:vytkni m2k2
59:rozloz podle vzorce x2-y2 (uz jsem to popisovat vyse)
Vsechny ty priklady jsou na jedno kopyto. Pouzivaji ty zakladni vzorce a vytykani. Musis to vice procvicovat, aby jsi vedela, ktere upravy jsou nejlepsi. To te doby zkousej ruzne upravy a budes sama videt, ktere vedou k jednodussimu zapisu a ktere naopak veci delaji jen slozitejsi.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.