Nejste přihlášen/a.
Dobrý den, mám za úkol příklady na rovnici hyperboly. Bohužel se mi nepodařilo přijít na to, jak to vyřešit, hledám řešení již od včerejšího večera.
Určete souřadnice středu hyperboly, délky poloos, excentricitu, souřadnice ohnisek a rovnice asymptot: 42−2+32−4+24=0
Předem děkuji za jakoukoli radu.
2x
Takže, tak, jak vidím zadání já, to skutečně neumím, ale podletoho, co vidí x, je to jinak.
Rovnice ze zadání je tedy
4x2 - y2 + 32x - 4y + 24 = 0
což upravím v duchu tazatelovy myšlenky (provedené korektně)
4(x2 + 8x) - (y2 + 4y) +24 = 0
4(x2 + 8x + 16) - (y2 + 4y + 4) +24 -16 +4= 0
4(x + 4)2 - (y+2)2 = -12
což po vydělení -12 v podstatě dá kýženou středovou rovnici. Mám pokračovat?
(omlouvám se, že používám spojovník místo minus, ale editor poradny mi to dovolí buď tak, nebo použít dlouhou pomlčku — . Co myslíte, že je lepší? Nelíbí se mi ani jedno.)
Dobře děkuji za odpověď, úkol mám skoro hotový, jediné co mi chybí jsou souřadnice ohnisek na ty nemohu stále přijít.
středová rovnice mi vyšla:
-(x2+4)2/3 + (y+2)2/12 = 1
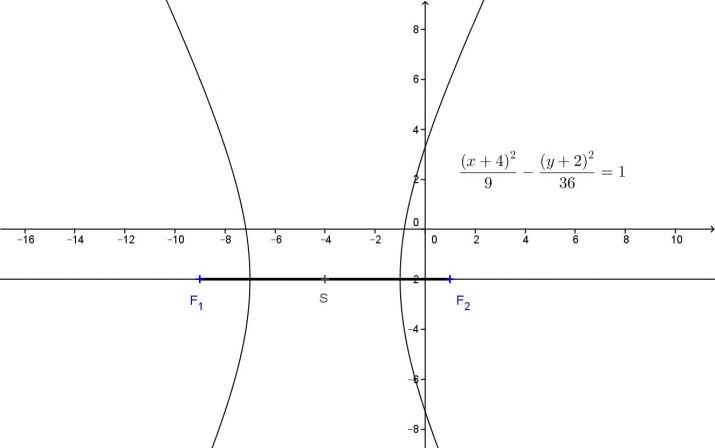
To není správné. Kartaginec se dopustil malého omylu, místo -16 má být -64 [= 4⋅ (-16)]. Takže po úpravě dostaneme rovici (x + 4)2/9 - (y + 2)2/36 = 1
Souřadnice středu jsou S = [-4; -2], poloosy a = 3, b = 6. Takže excentricita e = √(a2 + b2) = 5.
X-ová souřadnice ohnisek se pak o +5 a -5 liší od x-ové souřadnice středu.
To je opravdu moje nepřesnost, zakomněl jsem vynásobit. Ale bylo mi divné, že ve jmenovatelích nevycházejí kvadráty; není to sice povinnost, ale obvykle se tak příklady nekonstruují. Takže se moc stydím.
BTW omyl to byl, ale zda malý či velký, toť otázka, V každém případě jsem to měl špatne a to se počítá (nebo spíčš nepočítá ![]() )
)
A kdyby se x zaregistroval, už by měl další hodnocení.
Možná to bude znít špatně ale mně excentricita vychází 3 a ne 5.
e2 = 32 + 62 to celé pod odmocninou
e= 3
Omlouvám se, koukal jsem na špatné zadání excentricity, teď mi to je již jasné, a když teď potřebuji zjistit ohniska mohu pracovat s desetiným číslem?
Já bych to nechal v té podobě s odmocninou. Nač zbytečně vnášet do výpočtu zaokrouhlovací chyby, dokud opravdu nnemusím (a dokud nevím, jaká přesnost je potřeba).
Musím se také omluvit. Sice vztah pro výpočet excentricity mám dobře, ale neumím sčítat. 9 + 36 doopravdy není 25.![]()
Myslím si, že by se k sobě měly dát X a Y a odečíst 24 aby vzniklad následně na druhé straně jednička, tak aby vznikla středová rovnice hyperboly, ale opravdu nevím.
To byste tam nějaké X a Y musel mít. Nezlobte se, ale takto zadaný příklad je nesmysl; leda byste měl nějaký kontext, který by vysvětloval, co je co. Pro jistotu, aby nedošlo k nedorozumění, připojím snapshot toho, jak se mi příklad zobrazuje.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.