Zdravím, tak ještě jednou si dovolím pořádat o pomoc.
Naleznete geometricky (tj. nacrtnete a popiste konstrukci a urcete pocet reseni) v Gaussove rovine mnozinu bodu z splnujicich. nasledujici podminky:
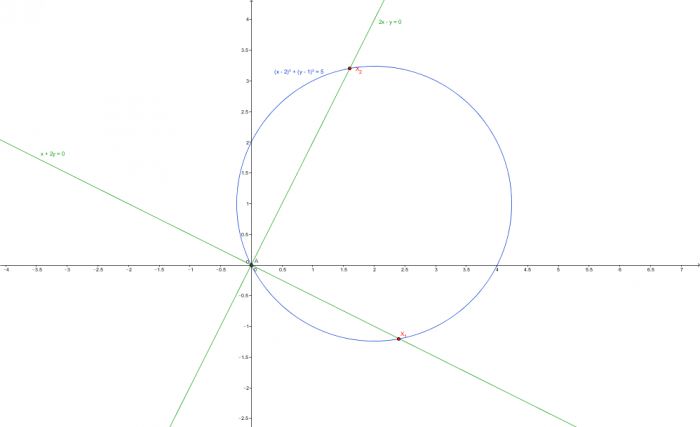
Re (2-i)/z . Im z/(2-i) = 0
|z-2-i|2 = 5
Reálná část by měla být souřadnice x a imaginátní y. Ale mate mě, že reálná i imaginární se skládá z podílu komplexních čísel.
Díky
2x
Co konkrétně vás mate? Obecně vzato, vyjdeme z toho, že z = z1 + iz2 = Re z + i Im z, dosadím do toho čísla (např. pro vyýpočet Im z/(2-i) napíšu z/(2-i) = z*(2 + i)/5 [standardní usměrňování] =(2z1 -z2) + i(z1 + 2z2) a tedy Im z/(2-i) = (z1 + 2z2). Následně dosadíme do podmínek. jestli to čtu dobře, tak podmínka je, že součin těch dvou výrazů je roven nule. Tedy buď (z1 + 2z2) = 0, což je rovnice nějaké přímky v Gaussově rovině. nebo Re (2-i)/z, což po úpravě bude zase nejaká přímka (sice tam máte z ve jmenovateli, ale nulovost (upraveného) zlomku je nulovost čitatele, jen nezapoeňte, že tato podmínka vám vylučuje z = 0). Takže ta druhá podmínka reprezentuje v Gaussově rovině nějaký šikmý kříž, první podmínka je rovnice kružnice (se středem 2+i a poloměrem √5) a s tím si už jistě poradíte.
doplněno 25.04.14 09:20:Takže stručně: reálná a imaginární část se neskládají z podílu komplexních čísel, ale berou se z tohoto podílu, který za tím účelem muséte upravit (usměrněním, roznásobením) na standardní aritmetický tvar.
Díky. No, problém je ten, že o komplexních číslech jsem nic nevěděl (co si pamatuju, tak na průmce před cca 20 lety jsme se o nich maximálně zmínili, že umožňují počítat záporné odmocniny a kvadratické rovnice se záporným diskriminantem) a teď musím počítat nějaké příklady. A něco ze základů jsem asi vstřebal, ale jednak mi chybí pokročilejší znalosti a druhak mi nejspíš něco dost zásadního uniká v představě o nich. Ať už v geometrické reprezentaci a nebo v tom, že jednou vystupuje v rozloženém tvaru a současně v "celém", Takže pak mám zmatek, jak s tím pracovat. Ale díky vám se snažím na příkladech i alespoň něco pochopit. (A něco snad i pochopil, i když to jde ztuha.)
Teď tedy, co jsem spočítal sám podle toho, jak jsem pochopil váš postup. U toho Re mi tím postupem vyšlo tohle, což je asi špatně, protože by to byl spíš prostorový, než rovinný útvar:
z/(2-i) = z.(2+i)/(2-i)(2+i) = (z1 + iz2).(2+i)/5 = 1/5((2z1 - z2) + i(z1 + 2z2))
Im z/(2-i) = 1/5(z1 + 2z2)
(2 - i)/z = (2 - i)/(z1 + iz2) = ((2z1 - z2)/(z12 + z22)) - i((z1 + 2z2)/(z12 + z22))
Re (2 - i)/z = (2z1 - z2)/(z12 + z22)
A nebo, pokud bysme brali, že je to jen reálná část, tak je to vlastně obdoba 1/x (resp. konkrétně 2/z), tedy asi hyperbola?
Čekám, že už si ze mě rvete vlasy a předpokládám, že tam mám nějaké fatální nesmysly.
Ale počítáte dobře, možná jen ten výsledek špatně interpretujete. Jí bych to popsal takto:
Vy vyšetřujete výraz w = (2 - i)/z a spočetl jste , že w = (2 - i)/(z1 + iz2) = ((2z1 - z2)/(z12 + z22)) - i((z1 + 2z2)/(z12 + z22)). To lze zapsat i tak, že w = w1+iw2, kde w1, w2 jsou reálná číslaq, w1 = Re w = ((2z1 - z2)/(z12 + z22)), w2 = Im w = ((z1 + 2z2)/(z12 + z22). To je O.K., ale teď se mi zdá, že vy pokládáde w1, w2, případně w za finální produkt, proto říkáte, že jde o prostorový útvar, případně něco ještě složitějšího na způsob hyperboly. No, ono je to tak, že w1 = w1(z1,z2) je skutečně reálná funkce komplexní proměnné z , což lze chápat i jeko reálnou funkci dvou reálných promenných z1, z2, a její graf je skutečně trojrozměrná varieta (plocha ve třírozměrném prostoru; o výraze w = w(z) bych raději moc nemluvil, zde jde o komplexní funkci komplexní proměnné (zde komnkrétně o meromorfní funkci), což je dost složitá disciplina, související s Taylorovými řadami a s mnoha dalšími pojmy, už jet to, že graf takovéto funkce by byla dvourozměrná varieta ve čtyřrozměrném prostoru, je dost hrozivé a strašidelné). Ovšem v zadání se neptají, so je to za funkci, ptají se jen, kdy je to funkce rovna nule; to znamená, že kduž si představíte graf té funkce jako jakousi plasttickou mapu, nebo přímo jako terén, tak hledáte v Gaussově rovině promenných z1, z2 nulovou vrstevnici; v matematice mluvíme také o hladině funkce, ale pořád je to to, co známe z kartografie jako vrstevnici na mapě.
Takže problém, respektive jeho část, ještě musíme zohlednit ten druhý výraz,) je, najít množinu bodů v Gaussove rovině, pro které platí
Re (2 - i)/z = (2z1 - z2)/(z12 + z22) = 0
čili po vynásobení výrazem (z12 + z22)
Ale počítáte dobře, možná jen ten výsledek špatně interpretujete. Jí bych to popsal takto:
Vy vyšetřujete výraz w = (2 - i)/z a spočetl jste , že w = (2 - i)/(z1 + iz2) = ((2z1 - z2)/(z12 + z22)) - i((z1 + 2z2)/(z12 + z22)). To lze zapsat i tak, že w = w1+iw2, kde w1, w2 jsou reálná číslaq, w1 = Re w = ((2z1 - z2)/(z12 + z22)), w2 = Im w = ((z1 + 2z2)/(z12 + z22). To je O.K., ale teď se mi zdá, že vy pokládáde w1, w2, případně w za finální produkt, proto říkáte, že jde o prostorový útvar, případně něco ještě složitějšího na způsob hyperboly. No, ono je to tak, že w1 = w1(z1,z2) je skutečně reálná funkce komplexní proměnné z , což lze chápat i jeko reálnou funkci dvou reálných promenných z1, z2, a její graf je skutečně trojrozměrná varieta (plocha ve třírozměrném prostoru; o výraze w = w(z) bych raději moc nemluvil, zde jde o komplexní funkci komplexní proměnné (zde komnkrétně o meromorfní funkci), což je dost složitá disciplina, související s Taylorovými řadami a s mnoha dalšími pojmy, už jet to, že graf takovéto funkce by byla dvourozměrná varieta ve čtyřrozměrném prostoru, je dost hrozivé a strašidelné). Ovšem v zadání se neptají, so je to za funkci, ptají se jen, kdy je to funkce rovna nule; to znamená, že kduž si představíte graf té funkce jako jakousi plasttickou mapu, nebo přímo jako terén, tak hledáte v Gaussově rovině promenných z1, z2 nulovou vrstevnici; v matematice mluvíme také o hladině funkce, ale pořád je to to, co známe z kartografie jako vrstevnici na mapě.
Takže problém, respektive jeho část, ještě musíme zohlednit ten druhý výraz,) je, najít množinu bodů v Gaussove rovině, pro které platí
Re (2 - i)/z = (2z1 - z2)/(z12 + z22) = 0
čili po vynásobení výrazem (z12 + z22)
Ale počítáte dobře, možná jen ten výsledek špatně interpretujete. Jí bych to popsal takto:
Vy vyšetřujete výraz w = (2 - i)/z a spočetl jste , že w = (2 - i)/(z1 + iz2) = ((2z1 - z2)/(z12 + z22)) - i((z1 + 2z2)/(z12 + z22)). To lze zapsat i tak, že w = w1+iw2, kde w1, w2 jsou reálná číslaq, w1 = Re w = ((2z1 - z2)/(z12 + z22)), w2 = Im w = ((z1 + 2z2)/(z12 + z22). To je O.K., ale teď se mi zdá, že vy pokládáde w1, w2, případně w za finální produkt, proto říkáte, že jde o prostorový útvar, případně něco ještě složitějšího na způsob hyperboly. No, ono je to tak, že w1 = w1(z1,z2) je skutečně reálná funkce komplexní proměnné z , což lze chápat i jeko reálnou funkci dvou reálných promenných z1, z2, a její graf je skutečně trojrozměrná varieta (plocha ve třírozměrném prostoru; o výraze w = w(z) bych raději moc nemluvil, zde jde o komplexní funkci komplexní proměnné (zde komnkrétně o meromorfní funkci), což je dost složitá disciplina, související s Taylorovými řadami a s mnoha dalšími pojmy, už jet to, že graf takovéto funkce by byla dvourozměrná varieta ve čtyřrozměrném prostoru, je dost hrozivé a strašidelné). Ovšem v zadání se neptají, so je to za funkci, ptají se jen, kdy je to funkce rovna nule; to znamená, že kduž si představíte graf té funkce jako jakousi plasttickou mapu, nebo přímo jako terén, tak hledáte v Gaussově rovině promenných z1, z2 nulovou vrstevnici; v matematice mluvíme také o hladině funkce, ale pořád je to to, co známe z kartografie jako vrstevnici na mapě.
Takže problém, respektive jeho část, ještě musíme zohlednit ten druhý výraz,) je, najít množinu bodů v Gaussove rovině, pro které platí
Re (2 - i)/z = (2z1 - z2)/(z12 + z22) = 0
čili po vynásobení výrazem (z12 + z22)
(2z1 - z2) = 0
a to je rovnice přímky. Jen pozor, tato přímka prochází počíátkem, ale počátek musíme z řešení vyloučit, protože pro z = 0 bychom měli nulu ve jmenovateli.
Podobně siporadíme s tím druhým výrazem, s imaginární částí něčeho. a rozumím-li tomu dobře, klademe součin těchto výraů roven nule, řešením je tudíž množina všech bodů, pro které je jeden či druhý roven nule.
Díky moc, začínám alespoň matně tušit. Takže vlastně výsledkem Re (2-i)/z . Im z/(2-i) = 0 jsou 2 2 přímky procházející počátkem, jedna soupající a jedna klesající. To jsou vlastně 2 podpodmínky v jedné. Ta druhá podmínka je |z-2-i|2 = 5
Tam je možnost:
|z-2-i|2 = 5
(z-2-i)2 -5 = 0
z2 + 2z.(2 + i) + (-2 - i)2 -5 = 0
z2 + 4z + 2iz + 4 +4i +i2 = 0
z2 + 4z + 3 + i(2z + 4) = 0
kde je hodnota na reálné ose z2 + 4z + 3 a na imaginární ta závorka. A nebo druhá možnost, brát obsah absolutní hodnoty skutečně jako abs. hodnotu komplexního čísla, tedy √(a2 + b2). V tomto případě tedy:
|z-2-i|2 = 5
(√((z1 - 2)2 + i2(z2 - 1)2))2 = 5
(z1 - 2)2 - (z2 - 1)2 = 5
z12 - 4z1 +4 - z22 -2z2 + 1 - 5 = 0
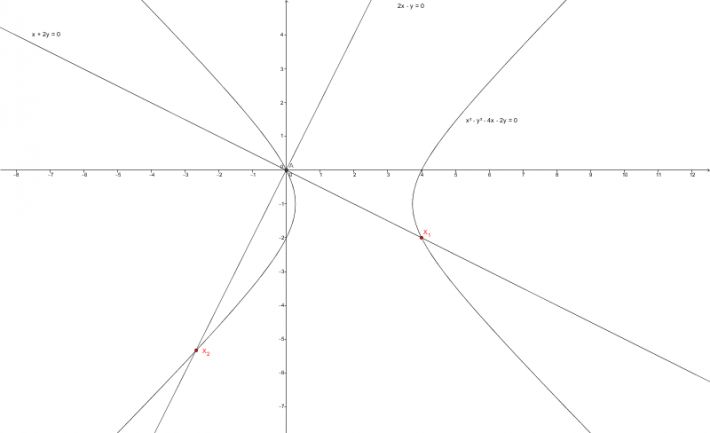
z12 - z22 - 4z1 - 2z2 = 0
Pak by výsledkem byla asi hyperbola?
Musím říct, že druhá verze se mni líbí víc, ale ruku do ohně bych za ni nedal.
doplněno 26.04.14 23:17:Pokud by platila druhá verze, byl by výsledek průnik oněch 2 přímek a hyperboly, Což mi vychází jako 3 body, jeden z nich počátek (a ten je vyloučen díky první rovnici). Je to možné?
doplněno 26.04.14 23:27:Tak ještě jednou a lépe... Nějak jsem tam blbě zadal přímky, takže by to mělo být spíš takto:
doplněno 26.04.14 23:29:Hm... Ten druhý obrázek není vidět, asi proto, že se jmenoval stejně, jako první. Tak do třetice.
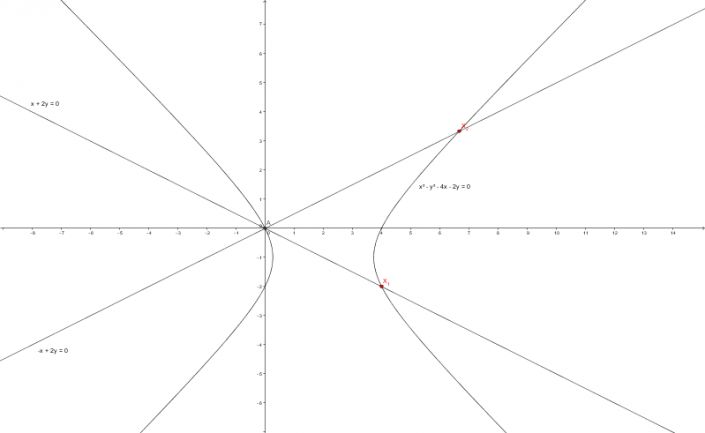


Jdete na to dobře, jen s tou absolutní hodnotou jste trochu vedle. Absolutní hodnota komplexního čísla je jeho vzdálenost od pošátku, normální euklidovská vzdálenost obrazu toho číslla od počátku. Takže absolutní hodnoota |z| čísla z = z1 + iz2 není odmocnina ze z12 + i2z22,ale ze z12 + z22, prostě vzdálenost bodu [z1,z2] od bodu [0,0]. Ono by možná stálo za to, povědět si více o zobrazení komplexního čísla a o Gaýussově rovnině, ale to by bylo na samoztatné povídání, snad jen řeknu stručně, že G. rovina má pro komplexní čísla analogický snysl, jako číselná osa psro čísla reálná. (Abs.hodnota |z| čísla z = z1 + iz2 se řečí komplexních čisel definuje vztahem |z|2 = (z1 + iz2) /(z1 - iz2), tedy její kvadrát jako součin čísla z a čísla komplexně združeného.) Jinak výraz |z-2-i|2 se dá přepsat jako |z-z0|2 , kde z0 = 2+i, a geometrocky to je vzdálenost bodu z od bodu z0, čili příslušný geometrický útvar bude kružnice. Ta další uvaha už je v podstatě dobře, jen ji musíte modifikovat s přihlédnutím k tomuto faktu.
Jinak já blbě vidím, takže tak úplně nepřečtu váš popis u těch přímek, ale mně vyšly k sobe kolmé.
doplněno 26.04.14 23:48:Jo. na tom opraveném obrázku je tak máte.
Díky moc!
To, že osy jsou reprezentantem částí jsem věděl (jako asi jednu z mála věcí), takže chápu, že to i tam vlastně nemusí být, je to symbol. Ale nějak mi to uteklo, jak to nemám začité. Takže chápu, že když se změní znaménko u z22 , tak máme rovnici kružnice (koeficienty u z12 a z22 mají stejnou hodnotu i znaménko). Takže výsledek je tohle: (za písmo se omlouvám, ale nepovedlo se mi GeoGebru donutit, aby dělala popisky větším písmem. Také si iniciativně přepsala rovnici kružnice do středového tvaru.)
Pokud myslíte, že je to dobře, tak ode mě to byl poslední příklad. I tak mi těch pár příkladů (nějaké jsem si tedy spočítal i sám) sebralo neuvěřitelně (a něúměrně) času. Díky moc za rady, podporu a neskutečnou trpělivost, strašně jste mi pomohl, bez vás bych to nevyřešil a nebo by to trvalo tolik času, kolik nemám.
doplněno 27.04.14 08:59:PS: jak na to koukám, tak při počítání té kružnice (s původní chybou tedy hyperboly) se mi tam středová rovnice objevuje už 2 kroky před obecnou, ale vůbec jsem si toho nevšiml, jak jsem se soustředil na jiný tvar. ![]()
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.