Nejste přihlášen/a.
Sestrojte rovnostranný trojúhelník,je-li dán součet s délek jeho strany a výšky.
1x
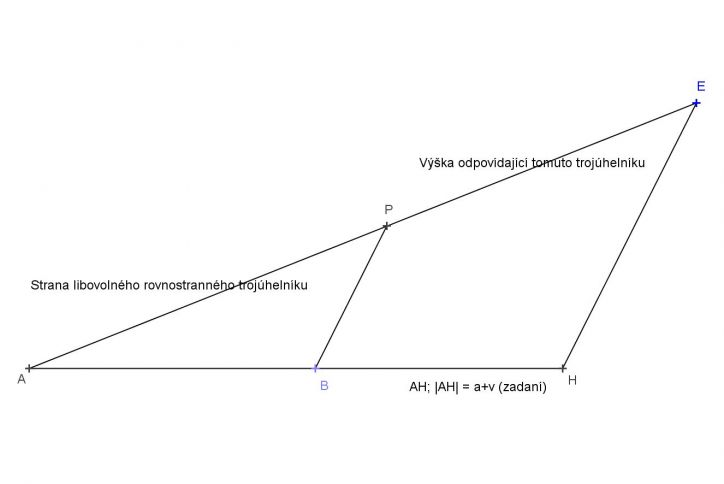
Řešení je prosté. Všechny rovnostranné trojúhelníky jsou si podobné, tak začnu tím, že zkonstruuji libovolný rovnostranný trojúhelník, dejme tomu ABC, v něm výšku třeba na stranu c, buíž to třeba úsečka CP. kde P je pata kolmice na stranu c, a někam tam zabuduji coučety strany a výšky, například na polopřímku s počátkěm C, opačnou k polopřímce CP, vynesu délku |AC| strany trojúhelníka, koncový bod označím D, takže |PD| je rovno součtu strany a výšky.. No a teď už stačí sestrojit obrazec podobný tomu, co jcem nakreslil, ale tak, že úsečka odpovídající PD bude mít délu s.
doplněno 25.04.14 08:38:x v příspěvku o cvě minuty starším rozkreslil podstatu této úvahy. Princim je stejná, jen se soustředil na konstrukci strany a, trojúhelník by následně kreslil s použitím tohoto výsledku. Dal bych mu bod, ale on ho nechce (není registrovánú.
Otázka trochu mimo mísu. Ten součet je s a v nadpise otásky je
bez číselných údajů
tak co ještě chcete vědět?
Většinou pokud je v zadání - je-li dáno, jsou tam stanoveny nějaké údaje. Pokud tedy součet v tomto zadání není uveden, nechápu, proč je tam je-li dáno...V tom případě je tedy úplně jedno kolik budou měřit strany toho trojúhelníku, musí býtvšak všechny 3 stejně dlouhé.
Nerozumím, čemu nerozumíte. Ten součet je dán a je roven s, s jo obecné číslo a nevím, co vám záleží na tom, jestli je dest centimetrů nebo 258 kilometrů, stejně to budete kreslit v měřítku. A strany hledaného trojúhelníka nebudou libovolné, musí být takové, aby (v aritmetickém vyjádřen) s = a(1+(3/2)√2), kde a je strana. Když to takhle neberete, zkuste si to třeba pro s = 12 cm a budete to umět obecně.
0x
Sestrojíme libovolný rovnostranný trojúhelník a sestrojíme úsečku, která bude součtem jeho strany a výšky. Poté zadanou úsečku o délce s rozdělíme na dvě části ve stejném poměru, jako je námi sestrojená úsečka.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.