Ahoj,
prosím o pomoc s následujícím příkladem:
Tři kamarádi chytali ryby. Arnošt chytil 20 % všech ryb a z toho 1/5 zlatých, Bonifác 50 % a z toho 1/10 zlatých a Cecil 30 % všech ryb a z toho 1/6 zlatých. Ryby pak nasypali na společnou hromadu a náhodně jednu vybrali. Jaká je pravděpodobnost, že ji chytil Bonifác, je-li rybka zlatá?
Prosím o vysvětlení, jak postupovat při řešení a jaký je výsledek.
Moc děkuju.
0x
Ahoj,
přikládám své řešení, nejsem si však 100% jistá, zda je to správně. Snad to tu někdo ještě zkontroluje, případně opraví.

Pravděpodobnost P = 0,14 je pravděpodobnost, že náhodně vybraná ryba ze společné hromady, je zlatá. Otázka však zní "Jaká je pravděpodobnost, že ji chytil Bonifác, je-li vybraná rybka zlatá?"
0x
Pravděpodobnost vytažení zlaté rybky označíme P(Z). Známe pravděpodobnosti
P(A) = 0,2 ... pravděpodobnost, že náhodně vybraná ryba je od Arnošta,
P(B) = 0,5 ... pravděpodobnost, že náhodně vybraná ryba je od Bonifáce,
P(C) = 0,3 ... pravděpodobnost, že náhodně vybraná ryba je od Ceccila.
Dále známe pravděpodobnosti
P(Z|A) = 1/5 ... pravděpodobnost chycení zlaté rybky Arnoštem,
P(Z|B) = 1/10 ... pravděpodobnost chycení zlaté rybky Bonifácem,
P(Z|C) = 1/6 ... pravděpodobnost chycení zlaté rybky Cecilem.
.
Hledáme pravděpodobnost P(B|Z), že náhodně vybraná ryba je chycená Bonifácem za podmínky, že vybraná ryba je zlatá. Můžeme použít Bayesův vzorec:
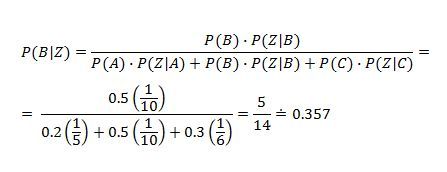
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.