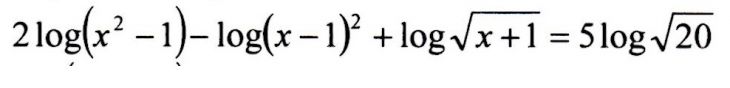Zdravím všechny ochotné poradit . Učím se logaritmy a nevím si rady , jak postupovat . Zase mě nezajímá výsledek , ale jen postup, abych pochopil jak na ty příklady . Děkuji za rady .
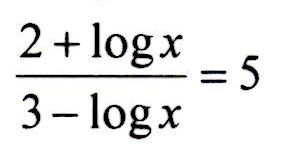
0x
Co tak pro jednoduchost místo log x uvažovat pouze jakési x a řešit rovnici jako normální rovnici o jedné neznámé. Vynásobit pravou stranu jmenovatelem levé a to bude 2+x= 5.(3-x) což je 2+x=15-5x a dále úpravami dojdeš až k 6x=13 a dělením šesti vyjde že x=2,5. Protože jsme x použili pro zjednodušení výrazu log x, je výsledek log x = 2,5, což si rozložíme na log x= 2+0,5. Protože se jedná o dekadický logaritmus, je číslo 2 logaritmus čísla 100 (má dvě nuly, proto ta dvojka) a násobené číslem, které má logaritmus 0,5. Z paměti to nevíš, tak se podíváš do tabulek a tam najdeš, že logaritmus 0,5 odpovídá asi tak číslu 7. Takže logaritmus 2+0,5 by měl patřit číslu 100.7=700... pokud v rychlosti uvažuju správně a dobře jsem to spočítal, pokud ne, omlouvám se...
díky za radu ,ale takovej postup mi ve škole neprojde a hlavně potřebuju natrénovat postupy pro další příklady . Hlavně počítat bez tabulek .
Až na to 13/6=2,5 (! ![]() ) celkem dobré.
) celkem dobré.
Pro @artik: Proč by ti ten postup neměl projít. Je to normální substituce log(x)=y (radši "y", psát zas "x" je trošku matoucí). Ale nemusíš to tak psát, jen ber ten log(x) chvíli jako celek a opisuj ho (takže rovnici např. vynásobíš členem 3-log(x)) a až se dostaneš na log(x)=13/6, tak ho jen vyčíslíš. A vy nesmíte u logaritmů používat tabulky? Ani kalkulačku?
Pro ten druhý případ bych asi použil poučky typu log(a)+log(b)=log(a*b), a*log(b)=log(ba) apod. A až bych dostal log(něco)=log(něcojiného), tak je jasné, že to "něco=něcojiného" (v rovnici log(x)=log(y) je jasné, že x=y, jinak by se nemohly rovnat ty logaritmy). Takže bych "log" vynechal a zbytek dořešil jako normální rovnici s jednou neznámou.
doplněno 13.04.14 15:41:Pro @artik: Pracuješ nepozorně. První příklad, vynásobení členem 3-log(x): 2+log(x)=15-5log(x). pak přičteš k oběma stranám 5log(x) a odečteš 2. A otázka: opsal jsi zadání tohoto příkladu dobře?
2. příklad: Dej sem svůj postup. Jako první krok bych navrhnul k oběma strnám přičíst log((x-1)2), jako druhý krok přehození činitelů 2 a 5 dovnitř logů (podle známé poučky), jako třetí krok pro každou stranu sločit součet logaritmů (o stejném základu) do jednoho logaritmu (podle známé poučky). Pak pokračovat dále.
Pro host: Vždyť jsem tě jinak za celý postup prochválil. Nesměju se ti, jen mě prostě ten přešlap pobavil. Stane se občas každému.
doplněno 13.04.14 15:45:pochválil, ne pRochválil
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.