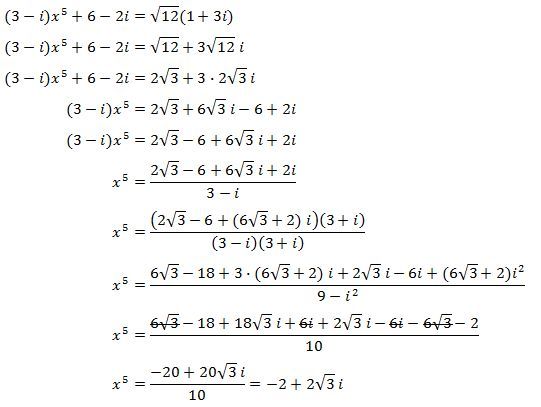Nejste přihlášen/a.
Už je mi to blbé, ale těch záseků mám dost. Příklad:
Naleznete vsechna komplexni reseni rovnice
(3 - i)x5 + 6 - 2i = √12 (1 + 3i)
v libovolnem tvaru.
Nevím, jak to zjednodušit. A co s rovnicí 5. stupně a ještě komplexní nějak moc nevím. Z tohohle tvaru mě nic nenapadá:
3x5 - ix5 = √12 + 6 + 3i√12 -2i
Když vyjádřím √12 jako 2√3 si moc nepomůžu. A cesta rozdělit to na 2 rovnice podle racionální a imaginární části asi taky nebude dobrá.
0x
Rovnici (3 - i)x5 + 6 - 2i = √12 (1 + 3i) lze upravit na tvar x5 + 2 - 2√3 i = 0 a dál ji řešit jako binomickou rovnici karlin.mff.cuni.cz/...
a vypočítat všechny n-té odmocniny z komplexního čísla -2 + 2√3 i.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.