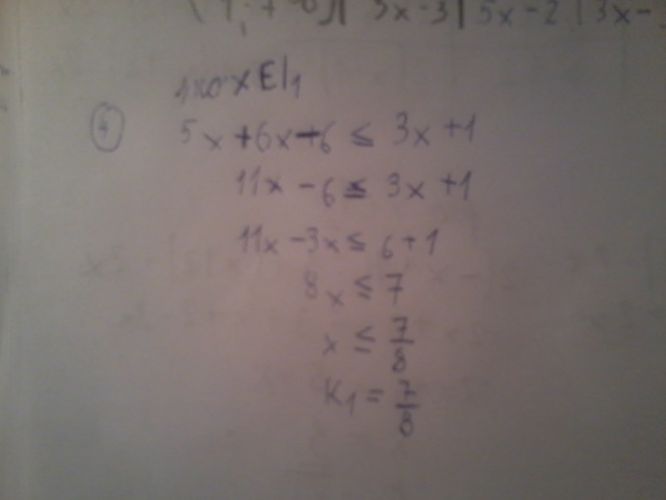Dobrý den, potřeboval bych poradit se dvěma příklady.
1.
Abych vypočítal příklad musím znát absulutní hodnotu.
absulutní hodnota z x+2 je x-2
absolutní hodnota z 1-x je kolik? X nesmí být mínus tak to bude x+1?------Této absulutní hodnotě nerozumím. Dál jsi tento příklad pak zvládnu dodělat sám.
2.
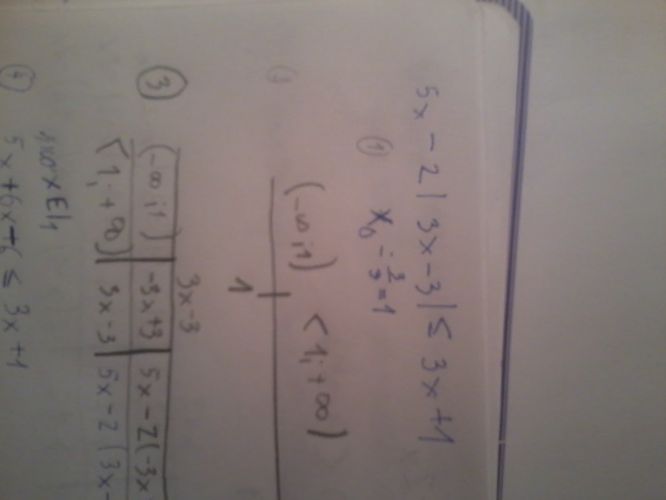
1. krok: určím absolutní hodnotu ___________________tady absolutní hodnota z 3x-3 je x+1. Budu mít tedy v příkladu jen jednu absolutníhornostu?
2. krok: ____pro představu si to zakreslím na osu________to umím
3.krok______ Tady jsi udělám tabulku _______jestliže znám obasolutní hodnoty tak to taky zvládnu
4. krok ______tady jsi sestavím rovnici________Tady mám trochu problém. Sestavím rovnici a vypočítám - tomu rozumím, ale pak se dělám ještě nějaká oso a tumu nerozumím.
5.krok_____tady udělám sjednocení
Moc Děkuji
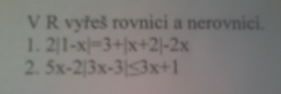
2x
? absulutní hodnota z x+2 je x-2?
2* |1-x| = 3+ |x+2| -2x
Teda, já bych to asi rozdělil na případy. 1-x: hraniční hodnota je 1, 1-x je nezáporné pro x<=1 (x je menší nebo rovno 1) - v tomto intervalu můžem abs. hodnotu nahradit závorkou, 1-x je záporné pro x>1, v tomto intervalu můžem abs. hodnotu nahradit mínus závorkou.
Obdobně x+2: nezáporné pro x>=-2, záporné pro x<-2.
Takže máme 3 významné intervaly: x<-2, x>=-2 a zároveň x<=1, x>1.
Pro interval x<-2 lze rovnici přepsat do tvaru: 2*(1-x)=3+(-(x+2))-2x
2-2x=3-x-2-2x
2-2x=1-3x
x=-1 a to NEvyhovuje výchozímu intervalu x<-2, tedy toto řešení není platné.
Pro interval x>=-2 a x<=1 lze napsat: 2*(1-x)=3+(x+2)-2x
2-2x=3+x+2-2x
2-2x=5-x
-3=x a to NEvyhovuje výchozímu intervalu x>=-2 a x<=1, tedy toto řešení není platné.
Pro interval x>1 lze napsat: 2*(-(1-x))=3+(x+2)-2x
-2+2x=3+x+2-2x
-2+2x=5-x
3x=7, takže x=7/3 a to VYhovuje výchozímu intervalu x>1, tedy toto řešení platné je.
Řešením celé rovnice je x=7/3.
Druhý příklad bych řešil obdobným postupem.
Prosím někoho dalšího, aby můj postup aspoň zběžně zkontroloval, jestli jsem někde ta znaménka a dosazování nezmotal. Princip je, doufám, použitelný.
Teď nevím, jestli si dobře rozumíme. Na tvou otázku říkám: ne. Absoutní hodnota je "operace", nebo funkce, předpis.
Toto |x+2| se nazývá "absolutní hodnota z x+2". Výsledek absolutní hodnoty je vždy nezáporný (kladný nebo 0). Ten samotný výraz x+2 má nulovou hodnotu při x=-2, zápornou hodnotu při x<-2 a kladnou hodnotu při x>-2. Výsledek absolutní hodnoty je nezáporný vždy.
Protože ten výraz sám je nezáporný pro x>=-2, tak pro tento interval x můžem klidně ty čáry absolutní hodnoty vynechat a napsat místo toho obyčejnou závorku.
Když je ale x<-2, tak ten výraz sám je záporný, absolutní hodnota mu ale převrátí znaménko (do plusu), takže je to to samé, jako když ho rovnou napíšeme s opačným znaménkem a zas pak můžem vynechat ty čáry absolutní hodnoty a napsat jen závorku (výsledkem tedy bude mínus závorka). Ale toto platí (v našem případě) jen v intervalu x<-2.
Takže |x+2| se dá rozepsat (můžeš si to snadno vyzkoušet):
|x+2| = -(x+2) pro x<-2; např. pro x=-100, |-100+2|=+98, -(-100+2)=+98
|x+2| = (x+2) pro x>=-2; např. pro x=70, |70+2|=72, (70+2)=72
Nejde tedy říct, že |x+2| (tedy absolutní hodnota z výrazu) je nějaké konkrétní x. Ale dá se třeba říct, že pro jedno konkrétní x=-2 je |x+2|=0, pro jiné konkrétní x=? bude výsledek té absolutní hodnoty jiný.
doplněno 28.03.14 11:04:Jinak ta (v našem případě) hodnota x=-2 je významná právě tím, že v ní se mění chování té absolutní hodnoty. Když pojedou x od této významné hodnoty na jednu stranu (v našem případě doprava), absolutní hodnota nebude měnit u vnitřního výrazu znaménko, pro x na druhou stranu znaménko výrazu měnit bude.
doplněno 28.03.14 11:25:Ten tvůj postup s tabulkou:
Pro I1 to máš dobře, vyšlo ti x=-1, takže protože to počítáš pro I1 od mínus nekonečna do -2, tak toto řešení rovnici nevyhovuje.
Pro I2 jsi na pravé straně zapomněl dvojku: 2*(-x+1)=3+x+2+2x.
A když se pak roznásobuje, tak 2*(-x+1)=-2x+2, ne -2x+1.
Pro I3 máš špatně úpravu rovnice:
2x-2=5-x ... přičtem x
3x-2=5 ... přičtem 2
3x=7
Jinak intervaly I2 a I3: ta +1 ještě patří do I2 a už nepatří do I3, protože (1-x) pro x=1 není záporné (absolutní hodnota nemusí otáčet znaménko), ale pro x>1 už je záporné (a absolutní hodnota znaménko mění na +); proto x=1 a x>1 nepatří do stejného intervalu.
1x
Jak na to koukám, tak trochu ano.
1) Pro x prvkem I1 máš x<=7/8. To je, zdá se, dobře. Jenže K1=7/8 už tak dobře není (jestli tedy nepoužíváte nějaké své dohodnuté značení). Ono se zde jedná o NErovnici a řešením této nerovnice není jen hodnota 7/8, ale interval od mínus nekonečna do 7/8 (včetně těch 7/8). Celý tento interval splňuje podmínku, že x je prvkem I1 (I1 je od mínus nekonečna do 1), takže je opravdu řešením.
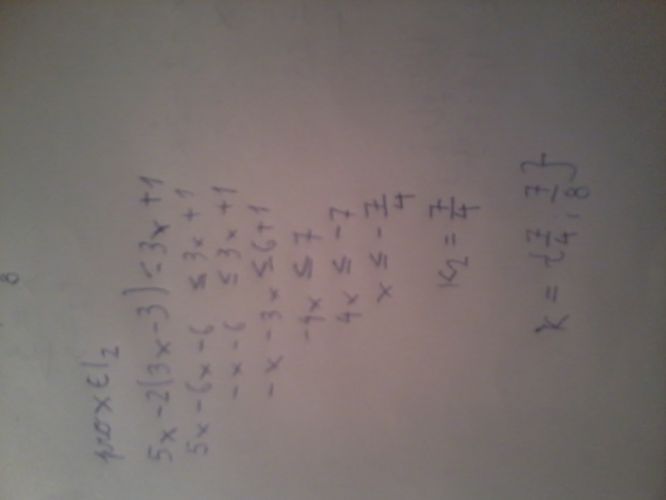
2) Pro x prvkem I2: druhý řádek má být 5x-6x+6<=3x+1, takže zbytek je jinak a vyjde to 5/4<=x. Musím tě ještě ale upozornit na další, tentokrát HRUBOU, chybu: -4x<=7 upravuješ na 4x<=-7. To nejde! Když se násobí NErovnice -1, musí se otočit ta nerovnost. Takže -4x<=7 se upraví na 4x>=-7. Je to stejné, jako bys přičetl k oběma stranám 4x a odečetl 7. Ale správně tam tedy vůbec -4x<=7 nevyjde.
No a výsledkem je zas interval. Řešením 5/4<=x je interval od 5/4 (to do něj patří) do nekonečna. A protože I2 je od 1 do nekonečna tak zas vyhoví celé to nalezené řešení.
Takže řešením jsou podle mne dva intervaly: mínus nekonečno až 7/8 (včetně) a 5/4 (včetně) až plus nekonečno.
doplněno 29.03.14 19:58:Jo a jak jsi vlastně přišel na K2=+7/4, když ti vyšlo x<=-7/4, to je mi záhadou. Ale stejně to nebylo dobře.
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.