Nejste přihlášen/a.
0x
To je hezké, a co s tím máme dělat? Znáte definici těch zde použitých norem, Pokud ano, tak do ní dosadíte a je to, takže asi všechnu neznáte. Co konkretně víte?
Tak když začnu od začátku, na ten první příklad jsem teď našel vzorec, tudíž by to mělo být odmocnina nad (2-(-3))2+(-2-(-2))2, u toho druhého nevím jak to použít.U toho třetího příkladu je ten 1+3t trojnásobkem toho prvního, tudíž to poroste 3x rychleji do +nekonečna od nuly? U toho čtvrtého a pátého si to neumím moc dobře představit.
Dobře, tak nejprve k té dvojce. Euklidovská norma ||u|| je skutečně součet čtverců souřadnic, následně odmocněný, čili pokud je u = (u1, u2, ,,,), tak ||u|| = (u12 + u22 + ...)½, no a protože Euklidovská vzdálenost dvou bodů nebo i dvou vektorů je norma jejich rozdílu, dostáváme se k tomu vzorci, která jste použil. Ve druhém příkladu je použito jen jiné označení euklidovské normy: ||u||2 je totéž jako ||u||, tekže ten poslední podpříklad umíte. A ty dalčí normy? Norma ||u||1 je tak zvaná součtová norma a je definována předpisem ||u||1 = ( |u|1 + |u|2 +...), ktežto ta první norma je tzv. maximová norma a je definována tak, že vezmu absoludní hodnotu souřadnic a z nich vyberu maximální hodnotu; teď už to jistě snadno spočtete.
(Spíš pro zajímavost ta součtová a ta euklidovská norma jsou zvláštní případy p-normy pro p ≥ 1, definované předpisem
||u||p = (|u1|p + |u2|p +...)1/p,
a ta maximová norma se dá chápat jako limitní případ pro p jdoucí do nekonečna.)
K ostatnímu samostatně.
Třetí příklad" zne, přesněji vzato, směrový vektor dané přímky je takový že jeho druhá souřadnice je trojnásobkem první, ale to je z hlediska zadání nepodstatné. Tady jde o to, že pody dané přímky dostanu tak, že nechám t probíhat všechna reálná čísla, a otázka je, zda mazi těmito body je některý s těch vypsaných. Zkusme třeba bod [4, 3]. Porovnáním
4= 1 + t
dostanete t = 3, no a dosazení do 1+3t dostanete
1+3t = 10 , cež není 3 a tento bod na přímce neleží. Ostatní body ověřte sám.
Příklad 3: zde vám pomůže goniometrická jednotka. U prvních dvpuu příkladů je vzdálenost zkoumaného bodu od počátku rovna jedné, tak se pohybuje po kružnici a jde o to, jakou část z ní vyplní.
Čtyřka je malinko složitější, ale zkuste si to nakreslit a popřemýšlet.
doplněno 22.03.14 20:44:Ještě přidám, že vlastně jde o použítí polárních souřednic, jestli vám to pomůže.
doplněno 22.03.14 21:12:Abych vás ale zase nezmátl, to poyžití polárních souřadnic tam je, ale není to tak úplně přímočaré, berte to jako inspiraci-
Děkuji za rady, druhý a třetí příklad vyšel správně, zkusím se podívat na ten čtvrtý a pátý, kdyby mi to nevycházelo, tak se ještě ozvu. Každopádně prozatím velké díky!
Tak ten čtvrtý napíšu jak si myslím, že by měl být:
1) cos(2t) a sin(2t) v intervalu <0,π/2> dají čtvrtkružnici
2) cos(2t) a sin(2t) v intervalu <0,π> dají půlkružnici, tudíž by to mělo být tohle správně
3) 1-sin(t) a 2+cos(t) v intervalu <-π,π> si neumím moc představit, ale řekl bych, že to nebude půlkružnice
4) 2*cos(t) a sin(t) v intervalu <0,π> bych řekl, že je půlkružnice.
-----------------------------------------------
A připíši rovnou poslední příklad:
Aby se jednalo o uzavřený osmilístek, tak bych dosadil za A=4 a za B=2, takže osmilístek by měl být:
x=cos(4t)*cos(t)
y=cos(4t)*sin(t)
t je v intervalu <0,2π>
Můžete mi prosím zkontrolovat pravdivost mého řešení?
Není to tak docela. Teď jdu venčit, pak to upřesníatím jen tolik, že první tři příklady zobrazují kruhová oblouk, (u trojky se středem v bodě [1;2]), ale máte špatně tu velikost
doplněno 26.03.14 23:39:Tak podrobněji: označím-li úhel. který svírá radius vektor (průvodič) bodu [x;y] s osou x, písmenem α a vzdálenost tohoto bodu od počátku písmenem r, platí x = r cos α a y = r sin α.(To je princip polárních souřadnic.) Takže když v prvním příkladu z té čtyřky máte r = 1 α = 2t a t probíhá od nuly do ½π, tak α probíhá od nuly do π, což je půlkružnice. Bod 2 dává tedy kružnici, v trojce si posunete počádek a máte zase celou kružnici, s posunutým středem. (Sice je probýhána v opačném smyslu _ kvůli tomu mínusu _ ale na to se nikdo neptal.
V bodě 4 ten obrazec bode obíhat okolo počátku "do půlky" podobně jako by to byla půlkružnice, ale vzdálenost od počátku nebude konstentní. Zde plarí x2 + 4y2 = 4, což je rovnice elipsy.
A ten osmilístek máte dobře : tam musí být B = 2 (aby ten obrazec oběhl kolem dokola,) a A = 4.
(ještě to zkontroluji jednou, kdyy něco, pošlu opravu.)
doplněno 27.03.14 11:32:Opravuji, ta rovnice je
x2 + 4y2 = 4,
(neboli ¼ x² + y² = 1 )
A jo, já byl trochu napřed, polární souřadnice jsme začali brát až dnes. Každopádně děkuji za rady!
Jsem rád, pokud vám mé rady pomohly.
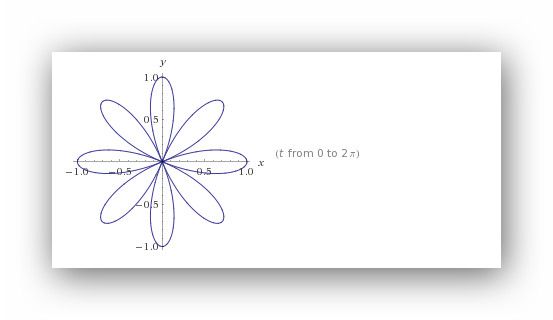
Pro zajímavost, ten osmilístek wolfram alfa vypočítal a nakreslil takto:
doplněno 28.03.14 18:06:Ten odkaz nějak nefunguje. Zkusím to znovu, a kdyby nefungovalo ani to, zkuste si sám do programu zadat výpočet výrazu
x = (cos 4t)*( cos t), x = (cos 4t)*(sin t), 0 < t < 2 &pi)
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.
