Nejste přihlášen/a.
Dobrý den
Potřeboval bych poradit ohledně Frekvenčních charakteristik.
Nikdy sem se s takovým případem nesetkal a potřeboval bych poradit jak na to, nebo popřípadě pomoc s prací.
"Vypočtěte zadání, pomocí frekvenčních chrakteristik:" 1) Amplitudová charakteristika (modulová char.)
2) Fázová charakteristika
3) Charakteristika v komplexní rovině
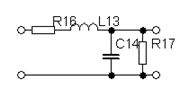
Obvod v příspěvku!
Zadané hodnoty:
R16 = 4K3 Ω
R17 = 4K7 Ω
C14 = 1200 pF
L13 = 2,44141E-05 H
3x
Tohle je priklad na reseni prenosove charakteristiky linearniho obvodu. Pokud neznate obecne postupy sestaveni obvodovych rovnic a neznate matematicke transformace (Laplaceova transformace) pro reseni a analyzu obvodu ve frekvenci oblasti nebude to pro vas lehke.
Jednodussi reseni asi pro vas bude vyjadrit si seriovou kombinaci R a L jako impedanci Z1 a paralelni kombinaci R a C jako Z2. Pak se to smrskne na impedancni delic. Prenos (frekvencni charakteristika) bude dan U2/U1=Z2/(Z1+Z2). Pak uz je to pocitani. Meli by vam vyjit 2 zlomove body na frekvencni charakteristice a tomu odpovidajici 4 zlomove body na fazove charakteristice.
Presne tak. Laplaceova transformace, impedancni delic (obecna verze odporoveho delice s obecnymi impedancemi). Pak si vyjadris napetovy prenos U2/U1, resp. pro logaritmickou prenosovou charakteristiku 20*log(U2/U1). Protoze to jsou komplexni cisla, tak ti vyjde zlomek 2 komplexnich polynomu. Absolutni hodnota tohoto komplexniho "cisla"je ta modularni ("modulo" = velikost komplexniho cisla) neboli amplitudova prenosova charakteristicka a argument (faze) komplexniho cisla je ta fazova charakteristika.
Vse jsou to samozrejme frekvencni charakteristiky, protoze frekvence je promenna tech funkci komplexni promenne.
0x
Nikdy neříkej nikdy, ale hledat. Pokud je to zadané ve škole, bylo to probíráno, je na to učebnice, odkazy.
search.seznam.cz/...=
search.seznam.cz/...
Neneseme odpovědnost za správnost informací a za škodu vzniklou jejich využitím. Jednotlivé odpovědi vyjadřují názory jejich autorů a nemusí se shodovat s názorem provozovatele poradny Poradte.cz.
Používáním poradny vyjadřujete souhlas s personifikovanou reklamou, která pomáhá financovat tento server, děkujeme.